Die Physik der Atmosphäre

Die Erde im Sonnensystem

Mit einem Anteil von 99,98% ist die Sonne der größte Energiespender unseres Planeten. Ihre Strahlung ist Ursache für die meisten energetischen Umwandlungsprozesse auf der Erde. Im Schnitt treffen $\unit[1367]{\frac{W}{m^2}}$ auf die der Sonne zugewandten Seite der Atmosphäre auf. Bezogen auf die ganze Erdhalbkugel sind das etwa $\unit[350]{PW}$ . In einer Stunde strahlt die Sonne somit über 2,5 mal soviel Energie ein, wie die gesamte Menschheit in einem Jahr verbraucht (Der Welt-Primärenergieverbrauch betrug nach [BMWI2008] im Jahr 2006 etwa $\unit[491,5]{EJ} \approx \unit[130]{PWh}$ ).

Bezogen auf ein Jahr werden etwa $\unit[1,5 \cdot 10 ^{18}]{kWh}$ von der Erde aufgefangen. Im Vergleich dazu waren im Jahr 1995 nach [Wuerfel1995] insgesamt nur $\unit[85,3 \cdot 10^{15}]{kWh}$ an “fossilen” (genauer: kohlenwasserstoffhaltigen) Energieträgern bekannt.

Verteilung der Solarstrahlung über die Erdoberfläche

Der ultraviolette Anteil des Sonnenlichts wird durch die Ozonschicht großteils absorbiert, der Rest der Strahlung durchdringt je nach Bewölkungsgrad die Atmosphäre und verteilt sich über den Planeten. Da die Umlaufbahn der Erde um die Sonne mit ca. $\unit[150 \text{ Mio.}]{km^{2}}$ wesentlich größer ist als der Durchmesser der beiden Himmelskörper [1], verlaufen auf der Erde einfallende Strahlen einfallende Strahlen nahezu parallel.

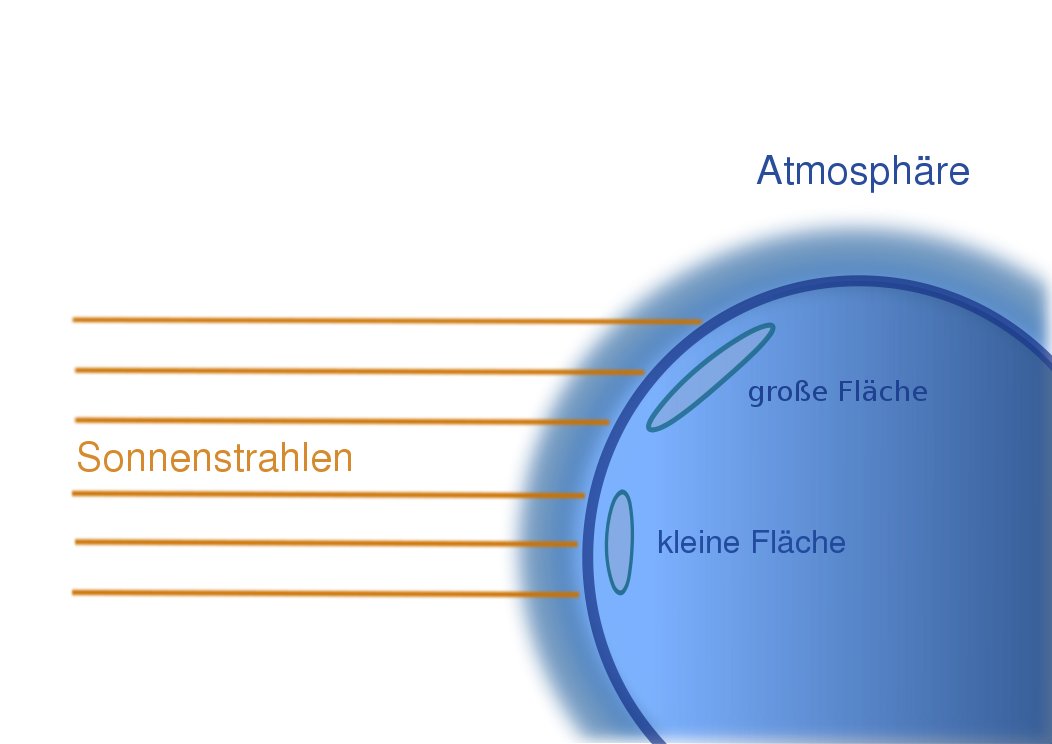
Die Kugelgestalt der Erde hat zur Folge, dass einfallende Strahlen unterschiedlich lange Wege durch die Atmosphäre zurücklegen müssen und auf unterschiedlich große Flächen treffen (vgl. Abbildung: Verteilung der Solarstrahlung). Somit kommt es zu unterschiedlicher Erwärmung der Atmosphäre und, da das Volumen von Gasen von der Temperatur abhängt, zu unterschiedlichem Luftdruck. Diese wiederum sind Ursache von Winden und Meeresströmungen, welche die räumlichen Temperaturdifferenzen auf der Erde teilweise ausgleichen.

Um eine letzte Vorstellung von der Dimension der Sonne zu bekommen: Licht benötigt für die Entfernung Sonne-Erde etwa acht Minuten, wobei es die Erde in einer Sekunde sechs mal umkreisen kann. Für weitere ca. 4,57 Milliarden Jahre wird der Erde die Sonne als gigantischer Energiespender erhalten bleiben.

Zirkulationsmuster auf der Erde

Globale Zirkulation

Die auftreffende Strahlungsenergie über ein Jahr gemittelt ist am Äquator am größten zu höheren Breitenkreisen hin ab: An den Polen steht innerhalb eines Jahres nicht einmal die Hälfte der Energie zur Verfügung, welche die äquatorialen Breiten erhalten. (Siehe auch Abschnitt Statistische Analyse von Solardaten.)

Die größte Differenz stellt sich zwischen 40° und 60° nördlicher bzw. südlicher Breite ein. Deutschland, mit seiner Breitenlage von 45° bis 55° Nord, liegt genau in diesem Bereich. Hier entspricht die eingestrahlte Solarenergie mit etwa $\unit[1000 \text{ bis } 1200]{kWh}$ je Quadratmeter und Jahr etwa dem haushältlichen Elektrizitätsverbrauch eines Bundesbürgers ([BMWI2008], [Hupf2005]).

Ohne die Schiefe der Ekliptik [2] und der Eigendrehung der Erde würde die am Äquator aufsteigende Luft in der Höhe nord- bzw. südwärts zu den Polen strömen und in Bodennähe relativ gleichmäßig zurückfließen. In der Realität verursachen jahreszeitliche Schwankungen und rotationsbedingte Scheinkräfte wie die Coriolis- und Zentrifugalkraft ein deutlich komplizierteres Muster (siehe Abbildung: Allgemeine Zirkulation). Diese grundsätzlichen Strömungstendenzen werden als ‘allgemeine Zirkulation’ bezeichnet.

Bodennahes Strömungsschema auf der Erde (vereinfacht). Quelle: [Klose2008]

Innertropische Konvergenzzone und Hadley-Zellen

Betrachtet man bodennahe Strömungsverhältnisse, so findet sich in den Tropen eine weitgehend zusammenhängende Tiefdruckrinne, in welcher die Passat-Winde zusammenströmen und in vertikale Luftbewegung übergehen. Da diese sogenannte Innertropische Konvergenzzone (ITC) von der solaren Einstrahlung abhängt, verlagert sie sich im Jahresverlauf: Im Nord-Sommer liegt sie nördlich, im Süd-Sommer südlich des Äquators. Aufgrund von ungleichen Land-Meer-Verteilungen auf den beiden Hemisphären liegt die ITC nach [Storch1999] im Mittel bei 5° nördlicher Breite.

Schematische Darstellung von Meridionalzirkulationen zwischen Pol und “Aquator. Mit ‘J’ sind der Polarfront- bzw. Subtropenfront-Jetstream eingezeichnet. Quelle: [Hupf2005]

Beiderseits der ITC schließen sich die sogenannten Hadley-Zellen an. In ihnen findet eine sehr stabile Zirkulation statt: In höheren Luftschichten wird polwärts strömende Luft aufgrund der Coriolis-Kraft ostwärts abgelenkt, in Bodennähe erfahren die als Passatwinde zurückströmenden Luftmassen nach dem gleichen Prinzip eine Westablenkung.

Aufgrund der polwärtigen Flächenkonvergenz der Erde werden vom Äquator wegströmende Luftmassen zunehmend verdichtet und in etwa bei 30° N bzw. 30° S zum Absinken gezwungen. In Bodennähe bilden sich dadurch die sogenannten ‘Suptropischen Hochdruckgürtel’ aus.

Ferrel-Zellen (Westwinddrift)

In den mittleren Breiten nimmt die Coriolis-Kraft stark zu (siehe Abschnitt Erdrotation). Dadurch werden die resultierenden Bewegungsablenkungen von polwärts strömender Luft nach Osten hin deutlich größer. Speziell im oberen Teil der Troposphäre treten mit großer Häufigkeit (im Norden) zwischen 30° und 40° Breite bzw. zwischen 50° und 75° Breite sogenannte Subtropen- bzw. Polarfront-Strahlströme (Jetstreams) auf: Tausende Kilometer lange, starke Westwinde, welche nahezu parallel zu den Linien gleichen Drucks verlaufen. In ihnen sind Windgeschwindigkeiten zwischen $\unit[100 \text{ und } 250]{\frac{km}{h}}$ üblich, es werden sogar Geschwindigkeiten bis zu $\unit[540]{\frac{km}{h} }$ gemessen ([Malberg2007]).

Abhängigkeit der Coriolis-Kraft von der geographischen Breite bei meridionaler Bewegung. Die angegebenen (Bahn-)Geschwindigkeiten entsprechen der Drehgeschwindigkeit der Erde. Quelle: [Hupf2005]

Diese sogenannten Ferrel-Zellen, häufig auch als Westwindzone oder Westwinddrift bezeichnet, werden durch die Kombination von starken Westwinden und großräumigen Temperaturschwankungen zwischen warmer Tropenluft und kalter Polarluft leicht instabil. An den “Polarfronten” kommt es zu unregelmäßigen Wirbelbildungen, und damit zur Entstehung von Tiefdruckgebieten (Zyklonen). Sie sorgen für eine effektive Durchmischung der unterschiedlich temperierten Luft.

Die Polarzelle: Polare Ostwinde

Die Polarfronten sind zwar kein geschlossenes Band um eine Halbkugel, stellen aber die Grenze zu den Polarzellen dar. Ihre vertikale Mächtigkeit beträgt etwa $\unit[1]{km}$ , bei einer mittleren Neigung von 1:100 ([Klose2008]). Auch sie unterliegen einem ständigen Mäandrieren und jahreszeitlichen Schwankungen.

Die Polarzellen stellen stabile, wenn auch schwach ausgebildete Strukturen dar. Äquatorwärts strömende Luft, welche die Polarkreise (66,5° N/S) erreichen, wird soweit erwärmt, dass sie aufsteigt. In der Höhe steht dem eine entsprechende Gegenströmung mit Absinken in der polaren Region gegenüber.

Regionale Einflüsse

Im Regionalklima wird das übergeordnete, großräumige Klimasystem durch regionale Besonderheiten beeinflusst. So spielt beispielsweise die Land-Meer-Verteilung eine wichtige Rolle, denn Ozeane reagieren aufgrund ihrer großen Wärmespeichervermögen wesentlich langsamer als das Festland auf thermische Veränderungen. Somit tragen sie v.a. in küstennahen Regionen sehr zur Stabilisierung des regionalen Klimas bei.

Die Nordhalbkugel ist zu 61%, die Südhalbkugel zu 81% von Wasser bedeckt ([Storch1999]). Auf der Nordhemisphäre kommt es daher zu stärkeren Abweichungen von dem allgemeinen Zirkulationsmuster als auf der Südhemisphäre.

Orographische Einflüsse, d.h. unterschiedliche Höhenstrukturen, führen zu lokalen Windzirkulationen sowie zu Luv- und Lee-Effekten. Bei der Überströmung von Gebirgen entwickeln sich (Schwere-)Wellen, gleichzeitig werden Strömungen abgelenkt. Speziell beim Schlingern (‘Mäandrieren’) der Westwindzone spielen diese Einflüsse eine bedeutende Rolle ([Klose2008]).

In jüngerer Zeit wird vermehrt auch untersucht, inwieweit der Mensch durch seine Aktivitäten das Klima beeinflusst, sei es durch Verdichtung von Städten, Abholzung von Wäldern, Ausstoß von Treibhausgasen, etc. Eine Diskussion dieser Effekte würde hier allerdings zu weit führen.

Meteorologische Bewegungsgleichungen

Grundgleichungen

Im Wesentlichen spielen fünf Kenngrößen für die Beschreibung von großräumigen Luftströmungen eine zentrale Rolle: Die Windgeschwindigkeit, der Luftdruck, die Lufttemperatur, sowie die Luftdichte und ihr Wassergehalt.

Die Gleichungen, welche die genannten Kenngrößen miteinander in Relation bringen, werden meteorologische Grundgleichungen genannt.

Bezogen auf eine Volumeneinheit lauten sie wie folgt:

Ideale Gasgleichung:

(1) $p = \rho \cdot R \cdot T$

Gleichung (1) stellt eine Vereinfachung der Van-der-Waals-Gleichung dar. [3] Sie beschreibt den linearen Zusammenhang zwischen Druck $p$ , Dichte $\rho$ und Temperatur $T$ . $R$ steht für die ideale Gaskonstante. Für eine trockene atmosphärische Zusammensetzung liefert Gleichung (1) gute Ergebnisse bei geringem Rechenaufwand. Wasserdampf wird gesondert behandelt.

Kontinuitätsgleichung:

(2) $\frac{\mathrm{d} \rho}{\mathrm{d}t} = -\rho \cdot \vec{\nabla} \cdot \vec{v}$

Gleichung (2) impliziert die Massenerhaltung. Der Nettofluss $\vec{\nabla} \cdot \vec{v}$ (Divergenz durch ein Volumenelement) muss gleich der zeitlichen Dichteänderung sein.

Wasserdampf-Bilanzgleichung:

(3) $\frac{\mathrm{d} \rho _{\rm{w}}}{\mathrm{d} t} = -\rho _{\rm{w}} \cdot \vec{\nabla} \cdot \vec{v} + \dot{W}$

Gleichung (3) liefert die Kontinuitätsgleichung für den Wasserdampf. Sie unterscheidet sich von Gleichung (2) insofern, dass es zu Feuchteänderungen durch Phasenübergänge (Niederschlag, Verdunstung) kommen kann. [4]

Erster Hauptsatz der Thermodynamik:

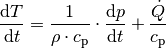
(4) $\frac{\mathrm{d} T}{\mathrm{d} t} = \frac{1}{\rho \cdot c_{\rm{p}}}\cdot \frac{\mathrm{d} p}{\mathrm{d} t} + \frac{\dot{Q}}{c_{\mathrm{p}}}$

Gleichung (4) beschreibt den Energieerhaltungssatz der Thermodynamik: Bei konstantem Volumen resultieren Temperaturänderungen entweder aus Druckänderungen oder aus einem Wärmestrom $\dot{Q}$ (Wärmezufuhr bzw. -abfluss). $c _{\rm{p}}$ steht für die spezifische Wärmekapazität eines Gases bei konstantem Druck.

Navier-Stokes-Gleichung: [5]

(5) $\rho \cdot \frac{\mathrm{d} \vec{v}}{\mathrm{d} t} = -\vec{\nabla} p + \rho \cdot \vec{g}_{\rm{s}} - 2 \cdot \rho \cdot \vec{\Omega} \times \vec{v} + \vec{\nabla} \cdot \vec{P} _{\rm{R}}$

Gleichung (5) entspricht dem 2. Newtonschen Axiom $\vec{F} = \frac{\mathrm{d}(m \cdot \vec{v})}{\mathrm{d} t}$ bezogen auf ein festes Volumen: Die Änderung des Geschwindigkeitsvektors $\vec{v}$ , multipliziert mit seiner Dichte, ist gleich der Summe der resultierenden Kräfte (Druckgradient, Schwerebeschleunigung, sowie Einfluss von Coriolis-Kraft und Reibung).

Auf die einzelnen Komponenten dieser zentralen Gleichung wird im folgenden Abschnitt ausführlicher eingegangen.

Den einzelnen Gleichungen kommen in der Praxis verschiedene Aufgaben zu. Die Navier-Stokes-Gleichung soll Auskunft über die zeitliche Entwicklung von horizontalen wie vertikalen Luftströmungen ergeben. Dazu sind Kenntnisse der Anfangs- und Randbedingungen nötig, die sich aus Modellannahmen, der Diagnose-Gleichung (1) und den übrigen Prognose-Gleichungen (2) bis (4) ergeben ([Kunz2006]).

Die Eulersche Gleichung

Zunächst soll die die Atmosphäre als ein ideales Fluid ohne Reibung ( $\eta=0$ ) betrachtet werden. Somit vereinfacht sich (5) zur sogenannten Eulerschen Gleichung:

(6) $\rho \cdot \frac{\mathrm{d} \vec{v}}{\mathrm{d}t} = - \vec{\nabla} p + \rho \cdot \vec{g}_{s} - 2 \cdot \rho \cdot \vec{\Omega} \times \vec{v}$

Gleichung (6) wird verständlicher, wenn man sich einige Spezialfälle ansieht.

Hydrostatische Grundgleichung und barometrische Höhenformel

Im einfachen Fall einer ruhenden und stabilen Atmosphäre verschwinden Windturbulenzen und die Coriolis-Kraft. Somit heben sich in Gleichung (6) die Druckkraft $\vec{F}_{\rm{D}}= \vec{\nabla} p$ und die Schwerkraft $\vec{F}_{\rm{S}}=\rho \cdot \vec{g}_{s}$ gegenseitig auf:

$\vec{\nabla} p = \rho \cdot \vec{g}_{\rm{s}}$

Mit $\vec{\nabla} = (\frac{\partial}{ \partial x},\frac{\partial}{ \partial y},\frac{\partial}{ \partial z})$ und $\vec{g}_{s} \approx (0,0,-g)$ lässt sich dabei die vertikale Komponente darstellen als}

(7) $\partial p = - \rho \cdot g \cdot \partial z$

Gleichung (7) wird als hydrostatische Grundgleichung bezeichnet: Der Luftdruck nimmt, da die Schwerebeschleunigung $\vec{g}_{\rm{s}}$ in negative $z$ -Richtung (zum Erdinneren) zeigt, mit zunehmender Höhe ab.

Setzt man in (7) für die Dichte $\rho$ die ideale Gasgleichung (1) ein, kann man die hydrostatische Grundgleichung auch wie folgt schreiben:

$\frac{\partial p}{p} &= - \frac{g}{R \cdot T} \cdot \partial z$

Die Integration über $\partial z$ ergibt:

(8) $\ln{p} = -\frac{g}{R\cdot T}\cdot z + C \qquad & \Leftrightarrow \qquad p = p_{0} \cdot e^{-\frac{g}{R \cdot T} \cdot z }$

Gleichung (8) heißt barometrische Höhenformel: Druck nimmt mit der Höhe, ausgehend von einem Grundniveau, exponentiell ab. Somit lässt sich beispielsweise berechnen, dass die Höhe, bei welcher der Luftdruck nur noch halb so groß wie in der Ausgangslage ist, bei etwa $\unit[5,54]{km}$ liegt ([Klose2008]).

Die Erdrotation: Zentrifugal- und Coriolis-Kraft

Da es sich bei der Erde um ein rotierendes Bezugsystem handelt, das zweite Newtonsche Axiom jedoch nur für Inertialsysteme gilt, treten in der Eulerschen Gleichung entsprechende Zusatzterme auf.

Wie auch allgemein für beliebige (Vektor-)Größen gültig lässt sich die Änderung eines festen Punktes auf der mit einer Winkelgeschwindigkeit von $| \vec{\Omega} | = \frac{2 \cdot \pi }{\unit[24]{h}}$ rotierenden Erdoberfläche in folgender Form schreiben:

$\left(\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right)_{\rm{IS}} = \vec{\Omega} \times \vec{r}$

Bewegt sich ein Teilchen auf der Erde, so summiert sich aus Sicht eines ruhenden Beobachters die ‘Führungsgeschwindigkeit’ mit der Relativbewegung:

$\vec{v}_{\rm{IS}} \; = \vec{\Omega} \times \vec{r} + \vec{v}_{\rm{Rel}}$

Für einen Beobachter auf der Erde erfährt die Bewegung dementsprechend eine scheinbare Ablenkung:

(9) $\vec{v}_{\rm{Rel}} \; &= \vec{v}_{\rm{IS}} - \vec{\Omega} \times \vec{r}$

Analog erhält man nach längerer Rechnung (siehe Abschnitt Scheinkräfte auf der Erde) für die Änderung der relativen Bewegung:

(10) $\left(\frac{\mathrm{d} \vec{v}}{\mathrm{d}t}\right)_{\rm{Rel}} = \left(\frac{\mathrm{d} \vec{v}}{\mathrm{d}t}\right)_{\rm{IS}} -2 \cdot \vec{\Omega} \times \vec{v} - \vec{\Omega} \times \vec{\Omega} \times \vec{r}$

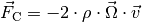Multipliziert man diese Gleichung mit $\rho$ , so wird auf der rechten Seite der Einfluss der beiden Scheinkräfte, der Coriolis-Kraft $\vec{F}_{\rm{C}}= -2 \cdot \rho \cdot \vec{\Omega} \cdot \vec{v}$ und der Zentrifugalkraft $\vec{F}_{\rm{Z}} = \rho \cdot \vec{\Omega} \times \vec{\Omega} \times \vec{r}$ deutlich.

Zentrifugalbeschleunigung und Erdrotation nach [Etling2008].

Die Zentrifugalkraft zeigt, wie in Abbildung: Zentrifugalbeschleunigung dargestellt, senkrecht von der Erdachse weg. Ihr Betrag ist mit $| \vec{F}_{\rm{Z}} | = \rho \cdot \vec{\Omega} \cdot \vec{\Omega} \cdot R_{\rm{E}} \cdot \sin{\vartheta}$ am Äquator am größten [6] und verschwindet an den Polen. Da die Zentrifugalkraft genauso wie die Gravitationskraft nur von der Position, jedoch nicht von der Relativgeschwindigkeit der Strömung abhängt, lassen sich beide Kräfte $\vec{F}_{\rm{G}}$ und $\vec{F}_{\rm{Z}}$ volumenbezogen zu einer effektiven Schwerkraft $\vec{g}_s$ zusammenfassen ([Pichler1986]):

(11) $\rho \cdot \vec{g}_s &= \rho \cdot \vec{g} + \rho \cdot \vec{\Omega} ^2 \cdot R_{\rm{E}} \cdot \sin \, \vartheta$

Die Zentrifugalbeschleunigung ist im Vergleich zur Gravitationsbeschleunigung gering [7], hatte allerdings erdgeschichtlich eine Abflachung des Planeten zur Folge ([Pichler1986]). Für die meisten atmosphärischen Betrachtungen genügt es jedoch die Schwerkraft näherungsweise gleich der Gravitationskraft zu setzen:

$\rho \cdot \vec{g}_{s} \approx \rho \cdot \vec{g}$

Auch die Coriolis-Kraft $\vec{F}_{\rm{C}}$ besitzt einen Einfluss auf vertikale Luftbewegungen. Bei reinen Aufwärtsbewegungen wirkt sie nach Westen, bei senkrechtem freien Fall nach Osten. Betrachtet man $\vec{v}_{\rm{x}}$ als Bewegung nach Osten, $\vec{v}_{\rm{y}}$ als Bewegung nach Norden und $\vec{v}_{\rm{z}}$ als Aufwärtsbewegung, so ergibt sich in Abhängigkeit vom Breitengrad $\phi$ mit dem Rotationsvektor der Erde $\vec{\Omega} = | \vec{\Omega} | \cdot (0, \cos\,\phi, \sin \,\phi)$ für die einzelnen Komponenten der Coriolis-Kraft:

(12) $\vec{F}_{\rm{C}}= -2\cdot \rho \cdot \vec{\Omega} \times \vec{v} = -2 \cdot \rho \cdot | \vec{\Omega } | \cdot \begin{pmatrix} 0 \\ \cos \,\phi \\ \sin \,\phi \\ \end{pmatrix} \times \begin{pmatrix} v_{\rm{x}} \\ v_{\rm{y}} \\ v_{\rm{z}} \end{pmatrix} = 2 \cdot \rho \cdot | \vec{\Omega } | \begin{pmatrix} \vec{v}_{\rm{y}} \cdot \sin \,\phi - \vec{v}_{\rm{z}} \cdot \cos \,\phi \\ \vec{ -v}_{\rm{x}} \cdot \sin \,\phi \\ \vec{v}_{\rm{x}} \cdot \cos \,\phi \end{pmatrix}$

Der Coriolis-Effekt ist am Äquator (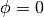 $\phi = 0$ ) gleich null und wird an den Polen mit $\unit[14,6 \cdot 10^{-4}]{\frac{1}{s}}$ maximal. Das liegt daran, dass ein Teilchen ohne Reibung seine anfängliche Bahngeschwindigkeit bis an den Zielort beibehält, gleichzeitig allerdings die Drehgeschwindigkeit der Erde, wie in Abbildung: Coriolis-Kraft dargestellt, infolge des geringer werdenden Radius abnimmt.

Bei rein horizontaler Luftbewegung $\vec{v}_{\rm{Hor.}} = (v_{\rm{x}}, v_{\rm{y}},0)$ sind auch nur die entsprechenden Komponenten der Coriolis-Kraft von Interesse. Sie lassen sich elegant schreiben als

(13) $\vec{F}_{\rm{C,Hor.}} = f_{\rm{C}} \cdot \rho \cdot (\vec{v}_{y},-\vec{v}_{x},0).$

Dabei wird $f_{\rm{C}}= 2 \cdot | \vec{\Omega} | \cdot \sin{\phi}$ als Coriolis-Parameter bezeichnet.

Geostrophischer und thermischer Wind

Betrachtet man nur konstante, horizontal verlaufende Luftströmungen, so vereinfachen sich die horizontalen Komponenten der Euler-Gleichung (6) zu:

(14) $\rho \cdot \frac{\rm{d}\vec{v}_{\rm{x}}}{\rm{d}t} &= -\frac{\partial p}{\partial x} +\rho \cdot f_{\rm{C}} \cdot \vec{v}_{\rm{y}} \\ \rho \cdot \frac{\rm{d}\vec{v}_{\rm{y}}}{\rm{d}t} &= -\frac{\partial p}{\partial y} - \rho \cdot f_{\rm{C}}\cdot \vec{v}_{\rm{\rm{x}}}$

Dabei wurde wieder näherungsweise $\vec{g}_{s} \approx (0,0,-g)$ gesetzt. Somit hat die Schwerkraft nur Auswirkung auf die vertikale Bewegung und taucht in den horizontalen Bewegungskomponenten nicht auf. Mit Hilfe des Coriolis-Parameters $f = 2 \cdot | \vec{\Omega} | \cdot \sin{\phi}$ ist die in Gleichung (14) genutzte, einfachere Schreibweise der Coriolis-Kraft möglich.

Beschleunigt ein Luftteilchen aus der Ruhe zunächst vom höheren zum tieferen Luftdruck, d.h. senkrecht zu den Isobaren, so tritt entsprechend der Strömungsgeschwindigkeit $\vec{v}_{\rm{Hor.}}$ die Wirkung der Coriolis-Kraft ein. Ursprünglich polwärts strömende Luft wird dabei nach rechts, äquatorwärts strömende Luft nach links abgelenkt.

Wirkung von Druck- und Coriolis-Kraft auf ein anfänglich ruhendes Luftteilchen, nach [Etling2008]

Im Laufe der Zeit stellt sich ein Gleichgewicht zwischen Druckkraft und Coriolis-Kraft ein. Die entlang paralleler Isobaren dann beschleunigungsfreie Luftströmung wird geostrophischer Wind genannt ([Malberg2007]). Für die Gleichgewichts-Situation ( $\mathrm{d} \vec{v} / \mathrm{d} t = 0$ ) gilt damit:

$\vec{v}_{\rm{x,geo}} &= -\frac{1}{p\cdot f_{\mathrm{C}}}\cdot \frac{\partial p}{\partial y}\\ \vec{v}_{\rm{y,geo}} &= +\frac{1}{p\cdot f_{\mathrm{C}}}\cdot \frac{\partial p}{\partial x }$

Ein geostrophischer Wind wird als ‘thermisch’ bezeichnet, wenn, wie meistens in der Realität, ein horizontales Temperaturgefälle die Ursache seiner Entstehung ist. Die Besonderheit des thermischen Windes liegt darin, dass sein Betrag mit der Höhe anwächst [Roedel2000]. Während am Boden überall ein relativ gleichmäßiger Luftdruck herrscht, nimmt der Druck in kalten Regionen schneller mit der Höhe ab als in warmen. An den Zonengrenzen stellt sich somit ein horizontales Druckgefälle ein, welches mit der Höhe zunimmt. In Abbildung: Aufbau der atmosphärischen Grenzschicht ist die Verschiebung der Niveaus gleicher Temperatur (Isothermen) gegen die Niveaus gleichen Drucks (Isobaren) graphisch dargestellt.

Zur Entstehung von Strahlströmen entlang einer Frontalzone. Die durchgezogenen Linien stellen isobare, die gestrichelten Linien isotherme Luftniveaus dar. Quelle: [Roedel2000]

Nach längerer Rechnung ([Roedel2000]) lässt sich aus den vorherigen Gleichungen die Abhängigkeit des thermisch bedingten geostrophischen Windes von der Höhe und dem horizontalen Temperaturgradienten berechnen. Verläuft beispielsweise der geostrophische Wind in $x$ – und die barokline Schichtung in $y$ -Richtung, so folgt für die Zunahme der Windgeschwindigkeit mit der Höhe:

(15) $\vec{v}_{\rm{x,geo}}(z) = \vec{v}_{\rm{x,geo}}(z_{0}) - \frac{g}{f_{c}\cdot T_{m}} \cdot \frac{\partial T_{m}}{\partial y}\cdot z$

$T_{m}$ steht für die über die Höhe $z-z_{0}$ gemittelte Temperatur.

Die im Abschnitt Ferrel-Zellen erwähnten Strahlströme in mehr als $\unit[10]{km}$ Höhe stellen markante Beispiele für geostrophische Windströmungen dar ([Malberg2007]). In Abbildung: Grenzschicht (Frontalzone) würden sie im oberen Bereich der Frontalzone senkrecht zur Papierebene verlaufen. (Vergleiche auch Abbildung: Meridionale Zirkulation.)

Die Strömungsrichtung der geostrophischen bzw. thermischen Winde parallel zu den Isobaren hat zur Folge, dass bestehende Druckunterschiede erhalten blieben. Erst zusätzliche Effekte, wie beispielsweise Reibung, bewirken eine Verschiebung des Gleichgewichts hin zu niedrigeren Druckflächen ([Simmer2003]).

Der Einfluss der Reibung

Infolge molekularer Kräfte besitzt jedes reale Fluid eine gewisse Viskosität (Zähigkeit). Der Einfluss dieser Kräfte wird in der Navier-Stokes-Gleichung (5) durch die Divergenz des Reibungstensors $\vec{P} _{\rm{R}}$ [8] beschrieben ([Pichler1986]):

(16) $\vec{P}_{\mathrm{R}} = 2 \cdot \eta \cdot \left[ \vec{D} - (\frac{1}{3}\cdot \vec{\nabla} \cdot \vec{v} ) \cdot E \right] + 3 \cdot \lambda \cdot (\frac{1}{3} \cdot \vec{\nabla} \cdot \vec{v}) \cdot E$

$\vec{D}$ steht dabei für den Deformationstensor, $\eta$ für den dynamischen Viskositätskoeffizienten. Mit $\lambda$ als Volumen-Viskositätskoeffizient berücksichtigt $(\vec{\nabla} \cdot \vec{v}) \cdot\/\vec{E}$ als Volumenviskosität die mögliche Energiedissipation durch Kompression oder Expansion in kompressiblen Fluiden.

Die Volumenviskosität ist einerseits direkt nur sehr schwer zu messen, andererseits verschwindet sie völlig in Gasen sehr geringer Dichte. Somit wird in der Praxis meist der Stokesche Ansatz genutzt, welcher von einem Verschwinden der Volumenenviskosität in Newtonschen Fluiden (s.u.) ausgeht ([Pichler1986]). Gase können oftmals tatsächlich in sehr guter Näherung als inkompressibel beschrieben werden ([Kuchling2004]). Damit verschwindet in Gleichung (16) die Divergenz, und der Reibungstensor vereinfacht sich zu:

(17) $\vec{P}_{\mathrm{R}} = 2 \cdot \eta \cdot \vec{D} = 2 \cdot \eta \begin{pmatrix} \tau _{\rm{xx}} & \tau _{\rm{yx}} & \tau _{\rm{zx}} \\ \tau _{\rm{xy}} & \tau _{\rm{yy}} & \tau _{\rm{zy}} \\ \tau _{\rm{xz}} & \tau _{\rm{yz}} & \tau _{\rm{zz}} \\ \end{pmatrix}$

Als Newtonsche Fluide werden Flüssigkeiten oder Gase bezeichnet, in denen die Schubspannungen $\tau _{\rm{ij}}$ proportional zu der jeweiligen Scherungsgeschwindigkeit sind. Für sie gilt:

(18) $\tau _{\rm{ij}} = \frac{1}{2} \left( \frac{\partial \vec{v}_{\rm{i}}}{\partial x_{\rm{j}}} + \frac{\partial \vec{v}_{\rm{j}}}{\partial x_{\rm{i}}}\right),$

Die angenommene Erhaltung des Volumens (Divergenzfreiheit) hat zur Folge, dass die Spur des Deformationstensors $\vec{D}$ verschwindet:

(19) $\mathrm{Sp}(\vec{D}) = \frac{\partial \vec{v}_{\rm{x}}}{\partial x_{\rm{x}}} + \frac{\partial \vec{v}_{\rm{y}}}{\partial y} + \frac{\partial \vec{v}_{\rm{z}}}{\partial z} = \vec{\nabla} \cdot \vec{v} = 0$

Weiterhin wird von isotropen Fluiden ausgegangen, d.h. eine Drehung des Gesamtvolumens kann unberücksichtigt bleiben. Daraus resultiert die Symmetriebedingung $\tau _{\rm{ij}} = \tau _{\rm{ji}}$ , und es bleiben fünf Freiheitsgrade für den Rotationstensor übrig.

Wie bei der Druckkraft kann damit die Reibungskraft $\vec{F}_{\rm{R}}$ je Volumeneinheit über die Divergenz des Reibungstensors beschrieben werden ([Pichler1986]):

(20) $\vec{F}_{\rm{R}}= \vec{\nabla} \cdot \vec{P}_{\mathrm{R}} = \frac{\partial \vec{P}_{\mathrm{R_{\mathrm{ij}}}}}{\partial x_{\rm{i}}}= \eta \cdot \left(\frac{\partial ^{2} \vec{v}_{\rm{j}}}{\partial x_{\rm{i}} \partial x_{\rm{i}}} + \underbrace{\frac{\partial ^{2}\vec{v}_{\rm{i}}}{\partial x_{\rm{i}}\partial x_{\rm{j}}}}_{=0}\right) = \eta \cdot \vec{\nabla} ^{2} \vec{v}$

Das Hinzufügen dieses nichtlinearen Reibungsterms zu der Euler-Gleichung (6) macht die Navier-Stokes-Gleichung (5) zu einer großen mathematischen Herausforderung. Noch heute ist nicht geklärt, ob sie überhaupt analytisch lösbar ist.

Aufbau der atmosphärischen Grenzschicht. Quelle: [Etling2008]

In der Realität ist vor allem die vertikale Veränderung der Reibung von Bedeutung. Unmittelbar oberhalb des Erdbodens findet in den ersten Millimetern aufgrund starker molekularer Wechselwirkungen nur laminare Strömung statt – die Luft ‘haftet’ förmlich am Boden.

In der darüberliegenden Prandtl-Schicht [9] , die witterungsabhängig bis in eine Höhe von 20 bis 100 Meter reicht, nimmt der Betrag der Reibung ab, überwiegt allerdings noch den Einfluss der Coriolis-Kraft ([Etling2008]). Somit ändert sich mit zunehmender Höhe der Betrag, nicht aber die Richtung der Windgeschwindigkeit.

Schließlich verliert in der Ekman-Schicht, die sich bis in Höhen von einem bis zwei Kilometern erstreckt, die Reibung immer mehr an Bedeutung, bis der Windvektor sich an den geostrophischen Wind der Atmosphäre anpasst.

Höhenprofile der bodennahen Grenzschicht

Die Höhe der Prandtl-Schicht ergibt sich daraus, dass in ihr turbulenzbedingte Flüsse höhenkonstant sein sollen. Dies ist bis in Höhen von etwa 20 bis 50 Metern der Fall ([Etling2008]). Die Abnahme der turbulenten Schubspannung wird aber auch durch Messungen in bis zu 100 Metern gefunden. Unter adiabatischen Verhältnissen stellt sich ein vertikales Profil logarithmisch anwachsender Geschwindigkeit ein:

(21) $\vec{v}_{\rm{Hor.}}(z) = \left(\frac{\vec{v}^{*}}{\kappa} \right)\cdot \ln{\left(\frac{z}{z_{0}}\right)}$

Hierbei ist $\vec{v}^{ *}$ die sogenannte Schubspannungsgeschwindigkeit [10], und $\kappa = 0,4$ die von-Karman-Konstante. Die Rauhigkeitshöhe $z_{0}$ gibt diejenige Höhe an, unterhalb welcher der Wind über einer spezifischen Oberfläche (theoretisch) auf null abgebremst wird. Um großflächigere, inhomogene Flächen zu beschreiben, werden verschiedene Landschaftstypen in Rauhigkeitsklassen eingeteilt. Die effektive Rauhigkeitshühe beträgt so für eine freie Meeresoberfläche $\unit[0]{cm}$ , für kleine Siedlungen $\unit[50]{cm}$ , für Großstädte mit Hochhäusern $\unit[200 \text{ bis } 250]{cm}$ , und für Europa als Ganzes ca. $\unit[90]{cm}$ ([Klose2008]).

Für neutrale Schichtungen lässt sich somit bei Kenntnis der Windgeschwindigkeit in einem Ausgangsniveau auf Windgeschwindigkeiten in anderen Höhen schließen. Für thermisch labile oder stabile Schichtungen kommt zusätzlich ein linearer Anteil hinzu:

(22) $\vec{v}_{\rm{Hor.}}(z) = \left(\frac{\vec{v}^{*}}\kappa \right)\cdot \ln\left(\frac{z}{z_{0}} + \alpha \frac{z-z_{0}}{L}\right)$

Ein gebräuchlicher Wert für die Konstante $\alpha$ ist $\alpha \approx 5$ , die Größe $L$ ist für die Prandtl-Schicht charakteristisch und wird Monin-Obukhov-Länge genannt ([Klose2008]). Wie in Abbildung: Schichtungsprofil zu sehen, nimmt die Windgeschwindigkeit bei labiler Schichtung ( $L<0$ ) gegenüber dem neutralen Fall mit der Höhe langsamer, bei stabiler Schichtung ( $L>0$ ) schneller zu.

Log-Linear-Profil der Windgeschwindigkeit für labile, neutrale und stabile thermische Schichtungen. Quelle: [Etling2008]

Die Vorticity

Um die Art und Intensität von Verwirbelungen in der Atmosphäre zu beschreiben, wird gerne die sogenannte Vorticitygleichung verwendet. [11]

Im folgenden werden horizontale Wirbel, deren Achse also in $z$ -Richtung zeigt, näher betrachtet.

Die Wirbelstärke (Zirkulation je Fläche) horizontaler Strömung ist wie folgt definiert ([Pichler1986]):

(23) $\vec\zeta = \left( \vec{\nabla} \times \vec{v} \right)_{z} = \frac{\partial \,\vec{v}_{\rm{y}}}{\partial x}-\frac{\partial \,\vec{v}_{\rm{x}}}{\partial y}$

Das Vorzeichen der Vorticity folgt der Rechtsschraubenregel: Bei einer Drehung im Uhrzeigersinn weist $\zeta$ in negative $z$ -Richtung (somit ist $\zeta$ negativ), bei einer Zirkulation gegen den Uhrzeigersinn ist $\zeta$ positiv. Vorticity, d.h. Zirkulation pro Fläche, tritt auf bei:

gekrümmten Bewegungen
geradlinigen Bewegungen mit horizontaler Scherung

Für eine starre Rotation um den Radius $\left| \vec{r} \right|$ gilt beispielsweise $\vec{v}=\omega \cdot \vec{r}$ . Mit dem Satz von Stokes [12] lässt sich daraus die Zirkulation $Z$

$Z = \oint \vec{v} \cdot \rm{d}\vec{s} = \vec{v} \cdot 2\cdot \pi \cdot \vec{r} = 2\pi \cdot \omega \cdot \vec{r} ^{2}=\int \vec{\nabla} \times \vec{v}\cdot \rm{d}A$

und somit $\zeta = (\vec{\nabla} \times \vec{v})_{z} = \frac{Z}{A}=\frac{Z}{\pi \cdot r^{2}}=2\omega$ berechnen ([Roedel2000]). Die Vorticity einer reinen Rotation ist somit gleich dem Doppelten der Winkelgeschwindigkeit.

Zur Herleitung einer Gleichung für die Wirbelstärke wird von der Navier-Stokes-Gleichung (?) ausgegangen. Für den Reibungsterm wird Gleichung (20) und für die Coriolis-Kraft Gleichung (13) eingesetzt. Zusätzlich wird die individuelle zeitliche Ableitung $\frac{\mathrm{d} \vec{v}}{\mathrm{d}t}$ mittels der “Eulerschen Zerlegung” in eine lokale Änderung $\frac{\partial \vec{v}}{\partial t}$ und einen Advektionsterm $\vec{v} \cdot \vec{\nabla} \vec{v}$ aufgespalten. (Siehe Die Eulersche Zerlegung)

(24) $\rho \cdot (\frac{\partial \vec{v}}{\partial t}+\vec{v} \cdot \vec{\nabla} \vec{v}) &= - \vec{\nabla} p +\rho \cdot \vec{g_{s}} - 2\cdot \rho \cdot \vec{\Omega} \times \vec{v} + \eta \cdot \vec{\nabla} ^{2} \vec{v}$

Wendet man entsprechend die Rotation auf die obige Form der Navier-Stokes-Gleichung an, so erhält man nach längerer Rechnung (siehe Herleitung der Vorticity-Gleichung)

(25) $\rho \cdot \left( \frac{\partial \zeta }{\partial t} + (\vec{v} \cdot \vec{\nabla} )\cdot (\zeta + 2\cdot \vec{ \Omega}) + (\zeta +2\cdot \vec{\Omega } ) \cdot (\vec{\nabla} \cdot \vec{v}) \right) - \eta \cdot \vec{\nabla} ^{2}\zeta = 0$

Die Erdrotation $\vec{ \Omega }$ (“planetare Vorticity”) und die Wirbelstärke $\zeta$ (“relative Vorticity”) können zu einer “absoluten Vorticity” $\zeta _{a}=\zeta +f_{c}$ zusammengefasst werden ([Etling2008]). Damit ergibt sich aufgrund der zeitlichen Konstanz der Erddrehung $\frac{\partial \vec{ \Omega }}{\partial t}= 0$ eine übersichtlichere Form von Gleichung (25):

(26) $\rho\cdot \left( \frac{\partial \zeta_{\rm{a}} }{\partial t} + \underbrace{(\vec{v} \cdot \vec{\nabla} )\cdot \zeta_{\rm{a}}}_{(1)} + \underbrace{\zeta_{\rm{a}} \cdot (\vec{\nabla} \cdot \vec{v})}_{(2)} \right) - \underbrace{\eta \cdot \vec{\nabla} ^{2} \zeta}_{(3)} = 0$

Term (1) wird als Dreh- oder Twistingterm bezeichnet. Er beschreibt, wie horizontale Vorticity beispielsweise durch Aufwinde in die Vertikale gekippt werden können. Insbesondere an Frontalzonen kommt es so zu einer effektiven Durchmischung warmer und kalter Luftmengen, woraus Instabilitäten entstehen. Diese wiederum begünstigen die Bildung von Zyklonen. Die aus der Höhe absinkende Warmluft führt am Boden zu einem Auseinanderströmen (Divergenz, Term (2)) der Luftmassen, welches nur durch die Reibung (Term (3)) begrenzt wird.

Thermische Zirkulation am Übergang einer Warm-Kalt-Front. Quelle: [Roedel2000]

Zusätzlich muss beachtet werden, dass aufgrund der Kontinuitätsgleichung (2) Divergenzen nur möglich sind, wenn dabei zeitliche Dichteänderungen auftreten. Teilt man Gleichung (24) durch die Dichte und wendet die Rotation unter Berücksichtigung von $\rho \neq \text{konst.}$ an, so tritt zusätzlich folgender, als Solenoidterm ([Etling2008]) bezeichneter, Vektor auf:

(27) $\vec{\nabla} \times \frac{1}{\rho } \vec{\nabla} p = - \frac{1}{\rho ^{2}} \cdot (\vec{\nabla} p \times \vec{\nabla} \rho )_{z}$

Gleichung (27) stellt abgesehen von Reibung die einzige Quelle für die Erzeugung bzw. Vernichtung von Vorticity dar. In einer barotropen Atmosphäre hingegen verschwindet mit der konstanten Dichte die Divergenz. Unter Vernachlässigung der Reibung stellt in diesem Fall die absolute Vorticity eine Erhaltungsgröße dar:

(28) $\rho \cdot ( \frac{\partial \zeta_{\mathrm{a}} }{\partial t} + \vec{v} \cdot \vec{\nabla} ) \stackrel{\eqref{eqn-eulerzerlegung}}= \frac{\mathrm{d}\zeta _{\mathrm{a}}}{\mathrm{d}t} = 0 \quad \rightarrow \quad \zeta _{\mathrm{a}} = konst.$

In Abschnitt: Planetarische Wellen wird sich zeigen, inwieweit die Erhaltung der (absoluten) Vorticity Einfluss auf Wellenbewegungen in der Atmosphäre hat.

Skalenanalyse

Um die Bedeutung der einzelnen Terme in den atmosphärischen Bewegungsgleichungen quantitativ abschätzen zu können, ist eine Skalen- oder Dimensionsanalyse hilfreich. Hierbei werden die einzelnen Glieder eines Gleichungssystems in Relation zu charakteristischen Vergleichsgrößen gestellt ([Pichler1986]).

Damit ergeben sich je nach Skalenbereich mehr oder weniger dominante, dimensionslose Magnituden:

(29) $\vec{v}= V\cdot \hat{\vec{v}} \qquad &\Leftrightarrow \qquad \hat{\vec{v}} = \frac{\vec{v}}{V}$

Charakteristische Größen werden als Großbuchstaben, Magnituden mit einem Dach gekennzeichnet. Analog zu (29) lassen sich auch entsprechende Masstäbe für räumliche Ausdehnung, Druck, Dichte, Zeit, usw. definieren. Der Nabla-Operator kann ebenfalls dimensionslos gemacht werden ([Pichler1986]):

(30) $\frac{\partial \vec{v}}{\partial x}=\frac{V}{L}\cdot \frac{\partial \hat{\vec{v}}}{\partial \hat{x}} \qquad & \Leftrightarrow \qquad \hat{\vec{\nabla} } = L \cdot \vec{\nabla}$

Wird die Navier-Stokes-Gleichung komponentenweise aufgeschrieben, lassen sich beispielsweise großräumige (synoptische) Bewegungen von Tiefdruckgebieten auf dominierende Terme untersuchen.

Charakteristische Größen atmosphärischer Bewegungen. $L$ bezeichnet die horizontale, $H$ die vertikale Ausdehnung. $T$ steht für die mittlere Durchgangszeit. Quellen: [Pichler1986], [Hupf2005]
Typ	$L \text{ in } \unit[]{m}$	$H \text{ in } \unit[]{m}$	$T \text{ in } \unit[]{s}$	Zeitraum
Kleinräumige Turbulenz	$10^{-2} \text{ bis } 10^2$	$10^{-2} \text{ bis } 10^2$	$10^{0}-10^2$	(Minuten)
Wolkencluster, Land-See-Wind	$10^{3} \text{ bis } 10^{4}$	$10^{3} \text{ bis } 10^{4}$	$10^{2} \text{ bis } 10^{3}$	(Stunden)
Wirbelstürme, Fronten	$10^{5} \text{ bis } 10^{6}$	$10^4$	$10^4 \text{ bis } 10^{5}$	(ca. 1 Tag)
Tief- und Hochdruckgebiete	$10^6$	$10^4$	$10^5$	(Tage)
Zonalströmung	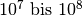$10^7 \text{ bis } 10^8$	$10^4$	$10^6$	(Wochen)

Mit charakteristischen Größen aus Tabelle: Skalen, üblichen Werten für Luftdichte $\rho \approx \unit[1]{\frac{kg}{m^3} }$ , Bodenluftdruck $p_{\rm{0}} \approx \unit[10^5]{Pa}$ und dem Coriolis-Parameter $f_{\rm{C}} \approx \unit[10^{-4}]{\frac{1}{s} }$ ergibt sich unter Vernachlässigung der Reibung für vertikale Luftbewegung:

(31) $\frac{\mathrm{d} \vec{v}_{\rm{z}}}{\mathrm{d} t} &= -\frac{1}{\rho} \cdot \frac{\partial p}{\partial z} -g + 2 \cdot \cos{\phi} \cdot \vec{\Omega} \cdot \vec{v}_{\rm{x}} + \vec{\nabla} \cdot \vec{P}_{\rm{z}} \\[6pt] \underbrace{\frac{V_{\rm{z}}}{T}}_{10^{-7}} &= \underbrace{-\frac{1}{\rho} \cdot \frac{p_{\rm{0}}}{H}}_{10} \underbrace{-g}_{10} + \underbrace{f_{\rm{C}} \cdot V_{\rm{x}}}_{10 ^{-3}}$

Der Einfluss der Coriolis-Kraft ist ebenso wie die Änderung der Vertikalgeschwindigkeit um einige Zehnerpotenzen geringer als Schwerebeschleunigung und Druckgradient, und kann daher vernachlässigt werden. Somit ergibt als Näherung die bereits bekannte statische Grundgleichung (7):

$\frac{\partial p}{ \partial z}= -\rho \cdot g$

Für die horizontalen Bewegungskomponenten erhält man analog:

(32) $\frac{\mathrm{d} \vec{v}_{\rm{x}}}{\mathrm{d} t} &= -\frac{1}{\rho} \cdot \frac{\partial p}{\partial x} + 2 \cdot \vec{\Omega} \cdot ( \sin{\phi} \cdot \vec{v}_{\rm{y}} - \cos{\phi} \cdot \vec{v}_{\rm{z}} ) + \vec{\nabla} \cdot \vec{P}_{\rm{x}} \\[6pt] \frac{\mathrm{d} \vec{v}_{\rm{y}}}{\mathrm{d} t} &= -\frac{1}{\rho} \cdot \frac{\partial p}{\partial y} - 2 \cdot \vec{\Omega} \cdot \cos{\phi} \cdot \vec{v}_{\rm{x}} + \vec{\nabla} \cdot \vec{P}_{\rm{y}} \\[6pt] \underbrace{\frac{V_{\rm{x}}}{T}}_{10 ^{-4}} &= \underbrace{-\frac{1}{\rho} \cdot \frac{p_{\rm{0}}}{L}}_{10 ^{-3}} \pm \underbrace{f_{C} \cdot V_{\rm{x}}}_{10 ^{-3}} - \underbrace{f_{\rm{C}} \cdot V_{\rm{z}}}_{10^{-6}}$

Unter Vernachlässigung kleinerer Terme gleichen sich Coriolis-Kraft und Druckkraft gegenseitig aus. Das Resultat ist eine geostrophische Windbewegung gemäß Gleichung (14):

$f_{\mathrm{C}}\cdot \vec{v}_{\mathrm{x}}=-\frac{1}\rho \cdot \frac{\partial p}{\partial y} \quad \text{bzw.} \quad f_{\mathrm{C}}\cdot \vec{v}_{\mathrm{y}}= \frac{1}\rho \cdot \frac{\partial p}{\partial x}$

Planetarische Wellen

In der Atmosphäre treten bei der Vielzahl an möglichen Strömungsmustern auch periodische Schwingungen und Kreisbewegungen auf [Etling2008]. Wirken beispielsweise außer der Coriolis-Kraft keine weiteren Kräfte, so lautet die Euler-Gleichung (6) für die $x$ – bzw. $y$ -Komponente:

(33) $\rho \cdot \frac{\mathrm{d} \vec{v}_{\mathrm{x}}}{\mathrm{d}t} - \rho \cdot f_{\mathrm{C}}\cdot \vec{v}_{\mathrm{y}} = 0 \qquad \text{bzw.} \qquad \rho \cdot \frac{\mathrm{d} \vec{v}_{\mathrm{y}}}{\mathrm{d} t} - \rho \cdot f_{\mathrm{C}}\cdot \vec{v}_{\mathrm{x}} = 0$

Beide Gleichungen lassen sich wie folgt zusammenfassen:

(34) $\frac{\mathrm{d}^{2} \vec{v}_{\mathrm{x}}}{\mathrm{d}\,t^{2}} + f_{\mathrm{C}}^{2} \cdot \vec{v}_{\mathrm{x}} = 0 \qquad \text{bzw.} \qquad \frac{\mathrm{d}^{2} \vec{v}_{\mathrm{y}}}{\mathrm{d}\,t^{2}}- f_{\mathrm{C}}\cdot \vec{v}_{\mathrm{y}} = 0.$

Obige Gleichungen haben die Form einer Wellengleichung. Wählt man als Ansatz für den harmonischen Oszillator $\vec{v}_{\mathrm{x}} (t) = \left|\vec{v}\right| \cdot \cos f_{\mathrm{C}}\cdot t \;$ bzw. $\;\vec{v}_{\rm{y}} (t) = -\left|\vec{v}\right| \cdot \sin f_{\rm{C}}\cdot t$ und nimmt die Coriolis-Kraft als näherungsweise konstant an, so ergibt sich als Lösung ein betraglich konstanter Windvektor, der sich im Uhrzeigersinn mit der Kreisfrequenz $\omega = f_{\rm{C}}$ dreht. [13]

Der Radius $R$ dieser sogenannten Trägheitskreise lässt sich berechnen, wenn man die resultierende Kraft $\rho \cdot \frac{\rm{d}\vec{v}}{\rm{d}t}$ in Gleichung (33) mit Hilfe der Skalenanalyse abschätzt ([Roedel2000]).

(35) $\vec{F} = \rho \cdot \left| \left( \vec{v} \cdot \vec{\nabla} \right) \cdot \vec{v} \right| \stackrel{\eqref{eqn:nablanodim}}\approx \rho \cdot \frac{\vec{v}^{2} }{R} = \rho \cdot f_{\rm{C}} \cdot \vec{v}$

Somit nimmt der Radius $R = \frac{ \vec{v}}{f _{\rm{C}}} = \frac{\vec{v}}{2 \cdot | \vec{\Omega} | \cdot \sin{\phi} }$ der Träheitskreise mit zunehmendem Breitenkreis ab. Die Umlaufdauer $T_{\rm{0}} = \frac{2 \cdot \pi \cdot R}{\vec{v}} = \frac{2 \cdot \pi }{f_{\rm{C}}}$ beträgt in Breiten um die 50° Nord bzw. Süd etwa 19 Stunden. Der zugehörige Trägheitsradius beträgt dabei etwa $\unit[45]{km}$ .

Teilchenbahn aufgrund des \beta-Effekts. Im Bereich A ist \vec{v}_{\rm{y}} > 0, und somit \mathrm{d} \zeta _{\rm{a}} / \mathrm{d} t< 0. Somit wird die Bahn antizyklonal und \vec{v}_{y} nimmt ab, bis sich im Bereich B eine umgekehrte Strömung einstellt. Analog wird die Bahn bei äquatorwärtiger Luftbewegung wieder zyklonaler, bis sich im Bereich C wieder die ursprüngliche Strömungsrichtung einstellt. Quelle: [Etling2008])

Geht man von einer barotropen Atmosphäre, d.h. konstanter Luftdichte aus, und vernachlässigt den Einfluss der Reibung, so stellt die absolute Vorticity, wie in Abschnitt: Die Vorticity gezeigt, eine Erhaltungsgröße dar. Dies hat zur Folge, dass bei einer polwärtigen meridionalen Strömung die relative Vorticity abnimmt, gleichzeitig allerdings die planetare Vorticity anwächst [Boljahn2009]. Im umgekehrten Fall einer äquatorwärtigen Bewegung erhält die Strömung durch die zunehmende relative Vorticity eine zyklonale Krümmung. Wird also eine geostrophische Windströmung aufgrund einer Störung (z.B. Gebirge oder unregelmäßige Verläufe zwischen Hoch- und Tiefdruckgebieten) abgelenkt, so setzt die breitenkreisabhängige absolute Vorticity als rücktreibende Kraft ein und hält die ursprüngliche Strömung aufrecht (vgl. Abbildung: Beta-Effekt).

Dieser Einfluss wird als $\beta$ -Effekt bezeichnet und lässt sich wie folgt beschreiben ([Etling2008]):

(36) $\frac{\mathrm{d} \zeta }{\mathrm{d} t} = - \vec{v}_{\rm{y}} \cdot \frac{\partial f_{\rm{C}}}{\partial y}$

Als Resultat ergibt sich für die Nordhalbkugel eine vom mittleren zonalen Grundstrom sowie dem Breitenkreis abhängige sogenannte Rossby-Welle. Als Dispersionsrelation ergibt sich nach [Boljahn2009] für die Phasengeschwindigkeit $C$ der Rossby-Welle:

(37) $C = \vec{v}_{\rm{x}} - \frac{f_{\rm{C}} \cdot L^{2}}{4 \cdot \pi ^{2}}$

Hierbei steht $L$ für die Wellenlänge der Rossby-Welle. Bei einer Breite von etwa 60° Nord liegt $L$ nach [Roedel2000] in etwa bei 7000 km. [14] Je kleiner die Wellenlänge ist, desto höher ist gemäß Gleichung (37) ihre Phasengeschwindigkeit. Da allerdings sowohl $\vec{v}_{\rm{x}}$ als auch $f_{C}\cdot L^{2}$ positiv sind, breitet sich die Welle stets langsamer als der Grundstrom aus. Bei besonders langen Wellen sind sogar negative Phasengeschwindigkeiten möglich.

In baroklinen Atmosphären gelten die für die Herleitung der Rossbywellen gemachten Annahmen nicht mehr. Kommt es dadurch zu Auslenkungensamplituden, welche größer als die Wellenlänge sind, so werden die planetaren Wellen schnell instabil, und es kommt zur Bildung von Zyklonen ([Boljahn2009]). Diese dauern gemäß Tabelle: Skalen ein bis drei Tage an und haben nach [Hupf2005] häufig Niederschläge sowie stärkere Windgeschwindigkeiten in der unteren Atmosphäre zur Folge.

Wettermodelle

Bis auf das ideale Gasgesetz (1) als reiner Diagnosegleichung sind alle meteorologischen Grundgleichungen partielle Differentialgleichungen der Zeit. Somit ist es grundsätzlich möglich bei bekannten Anfangsbedingungen mittels Integration auf künftige Zustände zu schließen. Hierauf beruht das Prinzip der numerischen Wettervorhersage ([Kunz2006]).

Aufgrund der weitreichenden Skalenbereiche werden hierbei verschiedene Größenordnungen meist getrennt betrachtet. Beispielsweise kann die Bildung einer Gewitterzelle an sich modellhaft beschrieben werden, sie wird bei der Berechnung von großräumigen Wetterlagen allerdings nur parametrisiert ([Balzer1998]).

Re-Analyse von Wetterdaten

Eine der Hauptschwierigkeiten in der Praxis der Wettervorhersage besteht darin, den Ausgangszustand der wichtigsten meteorologischen Größen hinreichend genau örtlich wie zeitlich zu bestimmen. Ein noch so gutes Prognosemodell liefert falsche Ergebnisse, wenn der Anfangszustand nicht gut genug beschrieben ist.

Das weltumspannende Messsystem für meteorologische Größen [15] umfasst zur Datenerfassung eine breite Palette an Datenlieferanten: Bereits zur Jahrtausendwende waren neben geostationären und polumlaufenden Satelliten etwa 700 Radarstationen, zahlreiche Driftbojen und Radiosonden, mehr als 4000 entsprechend ausgestattete Flugzeuge und Schiffe sowie über 10.000 Bodenmessstationen im Einsatz ([Balzer1998]). Jedes System hat Vor- und Nachteile: Dabei spielt neben Kosten, Messgenauigkeit und technischer Zuverlässigkeit auch eine Rolle, ob ein Messsystem punktuelle oder großflächige Messungen liefert und ob sie kontinuierlich oder in bestimmten Zeitabständen erfolgen.

Die Sammlung und Aufarbeitung aller dieser Messwerte wird als Datenassimilation bezeichnet. Ihr kommen mehrere Aufgaben zu:

kleinskalige Einflüsse sollen so weit als möglich herausgefiltert werden
aus möglicherweise widersprüchlichen Messwerten müssen die wahrscheinlichsten ausgewählt werden
fehlende Messwerte müssen ergänzt werden

Beispielsweise können eigentliche Strömungstendenzen der Luft von Böigkeiten oder Schwerewellen überlagert sein (meteorologisches “Rauschen”). Andererseits müssen die realen Aufenthaltsorte von Flugzeugen oder Driftbojen nicht unbedingt mit den theoretisch erwarteten Positionen übereinstimmen. Schließlich besitzen unterschiedliche Messtechniken verschiedene Genauigkeiten, und jederzeit können Messgeräte ausfallen.

Inzwischen erfolgt die Datenassimilation nahezu völlig automatisch. Immer mehr Daten werden dabei nahezu kontinuierlich mit ihrem Eintreten verarbeitet, nicht mehr in diskreten, beispielsweise stündlichen, Zeitschritten. Nach ([Balzer1998]) werden am Europäischen Zentrum für mittelfristige Wettervorhersage (EZMWF) [16] 37% der Computerzeit für das Assimilationssystem verwendet, während für die eigentliche 10-Tages-Prognose 9% ausreichen.

Energiebilanzmodelle

Die einfachste Art der Atmosphärenmodellierung durch sogenannte Energiebilanzmodelle (EBM) bietet eine erste Vorstellung der meteorologischen Praxis. Die Erde wird dabei als ganzes betrachtet oder in nur wenige Boxen unterteilt ([Storch1999]). Ziel ist es die Veränderung der Temperatur mittels des ersten Hauptsatzes der Thermodynamik in Abhängigkeit von solarer Einstrahlung, Albedo und Zusammensetzung der Atmosphäre zu beschreiben. Dynamische Prozesse spielen nur implizit eine Rolle.

Das ‘nulldimensionale’ EBM

Im einfachsten Fall wird in einem langfristigen, global gemittelten Modell angenommen, dass die eintreffende Bestrahlungsstärke der Sonne $E_{\mathrm{KW}}^{\downarrow}$ , die kurzwellige Rückstreuung $E_{\mathrm{KW}}^{\uparrow}$ und die langwellige Ausstrahlung $E_{\mathrm{LW}}^{\uparrow}$ sich im zeitlichen Mittel ausgleichen.

Gleichen sich die Energieflüsse nicht aus, ergibt sich eine von der Wärmekapazität $C_{\mathrm{w}}$ abhängige Temperaturänderung. Im ‘nulldimensionalen’ Fall, d.h. ohne horizontal oder vertikal räumliche Auflösung, orientiert man sich an dem Speichervermögen der Ozeane: Sie bedecken etwa 71% der Erdoberfläche und können über die obersten etwa 70 Meter verteilt Wärme speichern ([Storch1999]). Die Speicherkapazität der Landflächen ist dagegen vernachlässigbar klein. Somit lässt sich die Erdoberfläche als Ganzes näherungsweise als Energiespeicher mit einer effektiven Wassertiefe von 50 Metern beschreiben.

(38) $\frac{\mathrm{d}Q}{\mathrm{d}t}=C_{\mathrm{w}} \cdot \frac{\mathrm{d}T}{\mathrm{d}t} = E_{\mathrm{KW}}^{\downarrow} -E_{\mathrm{KW}}^{\uparrow} - E_{\mathrm{LW}}^{\uparrow }$

Die kurzwellige Einstrahlung $E_{\rm{KW}}^{\downarrow}$ ist über die Solarkonstante $E_{\rm{0}} = \unit[1367]{\frac{W}{m^2}}$ gegeben. Als Maß für das Rückstrahlungsvermögen wird ein global gemittelter Albedo-Wert angenommen, welcher derzeit bei etwa $\alpha = 0,3$ liegt ([Hupf2005]). Somit werden 30% der einfallenden Strahlung werden zurückgestreut:

$E_{\mathrm{\mathrm{KW}}}^{\uparrow} = \alpha \cdot E_{\mathrm{\mathrm{KW}}}^{\downarrow} = 0.3 \cdot E_{\mathrm{\mathrm{KW}}}^{\downarrow}$

Mit dem Stefan-Boltzmann-Gesetz, welches besagt, dass die Ausstrahlung eines Körpers von seinem Emissionswert $\varepsilon$ , seiner Fläche $A$ und der vierten Potenz seiner Temperatur $T$ abhängt, wird die langwellige Ausstrahlung $E_{\mathrm{LW}}^{\uparrow}$ parametrisiert:

$E_{LW}^{\uparrow} = 0,95 \cdot \sigma \cdot A \cdot T^{4} \cdot \tau$

Der Faktor 0,95 berücksichtigt die unterschiedlichen Emissionseigenschaften $\varepsilon$ der Erdoberfläche. Durch den Faktor $\tau$ findet der Treibhauseffekt, also die Reduktion der effektiven atmosphärischen Transmissivität, Berücksichtigung ([Klose2008]). Schließlich möchte man mit jedem Modell zunächst die Realität so gut wie möglich beschreiben. Die global gemittelte Jahrestemperatur der Erde, die es zu reproduzieren gilt, beträgt etwa 288 K. Damit ergibt sich für $\tau$ ein Wert von etwa 0,7.

Während die Erde über ihre gesamte Oberfläche $A=4 \cdot \pi \cdot R_{\mathrm{E}}^{2}$ Energie abstrahlt, kann sie nur entlang der Kreisfläche $\pi \cdot R_{\mathrm{E}}^{2}$ Solarstrahlung auffangen.

Zur numerischen Berechnung wird die in Gleichung (38) auftretende Zeitableitung als Differenz diskreter, aufeinanderfolgender Zeitschritte dargestellt.

(39) $C_w \cdot \frac{T_{\mathrm{i+1}}-T_{\mathrm{i}}}\Delta t \approx E_{\mathrm{KW}}^{\downarrow} -E_{\mathrm{KW}}^{\uparrow} - E_{\mathrm{LW}}^{\uparrow}$

Aufgelöst nach der Temperatur ergibt sich damit für den jeweils nächsten Zeitschritt:

$T_{\mathrm{i+1}} = T_{\mathrm{i}} + \frac{\Delta t}{C_{\mathrm{p}}}\cdot \left( (1 -\alpha ) \cdot \unit[1367]{\frac{W}{m^2}} \cdot \pi \cdot R_{\rm{E}}^{2} - 0,95 \cdot \sigma \cdot 4 \cdot \pi \cdot R_{\rm{E}}^{2} \cdot T_{\rm{i}}^{4} \cdot \tau \right)$

Der Term $(-0,95 \cdot \sigma \cdot T_{\mathrm{i}}^{4} \cdot \tau)$ führt zu einer negativen Rückkopplung: Abweichungen vom Gleichgewicht werden kompensiert, schnell pendelt sich ein stabiler Zustand ein ([Storch1999]).

Mehrdimensionale EBMs und Strahlungs-Konvektionsmodelle

Durch eine Auflösung der geographischen Breite und mehrerer übereinanderliegenden Atmosphärenschichten lässt sich das konzeptionelle, nulldimensionale Energie-Bilanzmodell in mehrere Dimensionen erweitern. Den einzelnen Modellvolumina werden individuelle Werte für Albedo, Transmissivität zugewiesen. Zusätzlich können Energietransporte durch eine Parametrisierung des Wärmeflusses zwischen einzelnen Zellen dargestellt werden.

Liegt der Vorteil von Energie-Bilanzmodellen in ihrer anschaulichen Vereinfachung, so liefern sie doch als Ergebnis zu warme Temperaturen in Bodennähe und zu niedrige Temperaturen in der oberen Atmosphäre ([Storch1999]). Konvektive Prozesse, die ebenso wie Strahlung zum Wärmetransport beitragen, werden in sogenannten Strahlungs-Konvektions-Modellen durch eine zusätzliche Parametrisierung der vertikalen Durchmischung berücksichtigt ([Etling2008]).

Während die Luftdichte mit der Zustandsgleichung für ideale Gase (1) einfach über den Luftdruck zu bestimmen ist, bereiten gerade die Auswirkungen turbulenter, subskaliger Verwirbelungen auf großskalige Strömungen Schwierigkeiten. Da sie nicht durch das räumlich diskrete Gitter erfasst und somit deterministisch berechnet werden können, wird die Parametrisierung zusätzlich stochastisch gewichtet ([Balzer1998]).

Globale Zirkulationsmodelle

Als rechenintensive Weiterentwicklung der Energiebilanzmodelle wurden allgemeine Zirkulationssysteme (General Circulation Model, GCM) mit komplett dreidimensionaler Auflösung zur Wettervorhersage entwickelt. Ziel dabei war und ist es, durch immer genauere Bestimmungen des Anfangszustands und immer feinmaschigere räumliche Diskreditierungen den möglichen Vorhersagezeitraum weiter auszudehnen.

Für eine numerisch fundierte Wettervorhersage von nur einem Tag sind Daten aus ganz Europa nötig. Für eine Vorhersage zwei bis vier Tage im Voraus benötigt man bereits Beobachtungen der ganzen Hemisphäre. Für fünf- bis siebentägige Prognosen müssen auch globale Einflüsse berücksichtigt werden ([Balzer1998]).

Das erste Modell des EZMWF im Jahr 1979 bestand aus 15 vertikalen Schichten mit einer horizontalen Auflösung von 1,875° geographischer Länge bzw. Breite, was entlang einem Großkreis einem Gitterpunktabstand von 200 km entspricht. 1997 gab es bereits 31 vertikale Rechenniveaus mit einer horizontalen Auflösung von ca. 60 km. Seit 2007 sind mittlerweile 5000 Super-Prozessoren im Einsatz, um täglich mehr als 300 Millionen Beobachtungsdaten rund um den Globus zu verarbeiten. Dabei werden 91 vertikale Flächen berücksichtigt, der horizontale Gitterpunktabstand beträgt 25 km ([EZMWF2007]).

Zur Verkürzung der Rechenzeit hat sich in den 1990er Jahren ein spektrales Berechnungsverfahren durchgesetzt. Jede periodische Funktion kann durch Fouriertransformation in eine Summe von Sinus- und Cosinuswellen zerlegt werden. Die horizontale Auflösung wird daher auch als Anzahl der auf einem Großkreis aufgelösten Wellen angegeben, beispielsweise T21, T213, oder aktuell: T799 ([EZMWF2007]). [17]

Grenzen der Wettervorhersage

Beinhalten Gleichungen nichtlineare Terme, so können Prozesse scheinbar regellose Lösungen haben, die empfindlich von Anfangswerten und Parametern abhängen. Zusätzlich können sich Modellfehler, Beobachtungsfehler und numerische Rundungsfehler mit zunehmenden Rechenschritten selbst bei einfachen Gleichungen anhäufen, was zu ‘deterministischem Chaos’ führt (siehe Abbildung: Deterministisches Chaos).

“Kollabieren” von Lösungen durch irreguläre Beobachtungsfehler (1), fehlerhaften physikalischen Modellierungen (2) oder Computerfehlern (3). Quelle: [Balzer1998]

Damit ist gemeint, dass auch bei bekannten zugrundeliegenden Regeln Lösungen zumindest innerhalb einer gewissen Schwankungsbreite auseinanderlaufen können.

In der meteorologischen Praxis bereitet v.a. die Bestimmung der vertikalen Geschwindigkeitskomponente Schwierigkeiten. Diese ist insbesondere für Wolkenbildung und Niederschlag von Bedeutung. Bei den meisten Messungen wird von der hydrostatischen Näherung ausgegangen, um beispielsweise Schallwellen herauszufiltern ([Balzer1998]). Dabei wird eine Messung der vertikalen Geschwindigkeit unmöglich.

Eine heute übliche Methode, diesen Problemen zu begegnen, stellen Vorhersage-Ensembles (Ensemble-Progose-System, EPS) nach dem Prinzip der Monte-Carlo-Methode dar:

Statistisch werden zufällig erzeugte Störungen in das Ausgangsfeld einkalkuliert. Diese Modelle mit unterschiedlichen Anfangsbedingungen, unterschiedlichen Parametrisierungen oder Kombinationen aus beidem werden parallel gerechnet und miteinander sowie mit aktualisierten Beobachtungsdaten verglichen.

Sind die Ergebnisse der Ensembles für einen Zeitraum der Prognose ähnlich und stimmen mit aktualisierten Beobachtungen überein, so ist das ein Indiz dafür, dass die Vorhersage für diesen Zeitraum relativ sicher ist. Im Gegensatz dazu werden Prognosen, welche den übrigen Vorhersagemodellen oder Beobachtungsdaten zu widersprechen scheinen, mit einer geringen Wahrscheinlichkeit gewichtet bzw. durch neue Rechenläufe ersetzt.

Während in einigen Fällen die Großwetterlage somit über 10 Tage recht gut prognostizierbar ist, gibt es andere Fälle, bei denen bereits nach wenigen Tagen eine zufriedenstellende Vorhersage kaum möglich ist ([EZMWF2007]).

Anmerkungen:

[1]	Die Sonne besitzt mit $\unit[1,39 \text{ Mio.}]{km}$ einen 109 mal so großen Durchmesser wie die Erde ( $\unit[6370]{km}$ ).

[2]	Als Ekliptik wird die Neigung der Rotationsachse der Erde gegenüber ihrer Bahnebene um die Sonne bezeichnet, siehe Abschnitt :ref`Die Ekliptik der Erde`

[3]	Für reale Gase lautet die van-der-Waalsche Zustandsgleichung: $(p + \frac{a}{v^{2}}) \cdot (v-b) = RT$ , wobei $a$ und $b$ Materialkonstanten sind. $\frac{a}{v^2}$ beschreibt die wechselseitige Anziehung der Moleküle, $b$ steht für das Eigenvolumen der Gase.

[4]	Das häufig für die absolute Luftfeuchtigkeit verwendete Symbol $f$ steht in diesem Werk für den Coriolisparameter. Um Verwechslungen zu vermeiden, wird für die Änderung der absoluten Feuchte (Masse Wasser / Volumen Luft) daher das Symbol $W$ verwendet.

[5]	Oft ist in der Literatur auch von Navier-Stokeschen Gleichungen die Rede. In diesem Fall ist die Gleichung komponentenweise für die drei Raumrichtungen dargestellt.

[6]	Für den Betrag der Zentrifugalbeschleunigung am Äquator gilt: $\left\| \frac{\vec{F}_{\rm{Z}}}{\rho} \right\| _{\rm{Max}} = \vec{\Omega} ^2 \cdot R_{\rm{E}} \approx \unit[3 \cdot 10^{-2}]{\frac{m}{s^2}}$

[7]	Für den Betrag der Gravitionsbeschleunigung gilt: $\vec{g} \approx \unit[9,8]{\frac{m}{s^2}}$ Selbst am Äquator ist die Gravitationsbeschleunigung somit rund 326 mal größer als die Zentrifugalbeschleunigung.

[8]	Die Begriffe Reibungstensor und (zäher) Spannungstensor sind identisch.

[9]	Die Prandtl-Schicht wird auch bodennahe Grenzschicht genannt, siehe Abbildung: Aufbau der atmosphärischen Grenzschicht

[10]

Die Schubspannungsgeschwindigkeit $\vec{v}^{*}$ stellt ein Maß für die Intensität des vertikalen Impulsstroms dar. Sie lässt sich aus Gleichung (21) bestimmen, wenn man $u(z)$ bei $z=2,7 z_{0}$ ermittelt: Mit $\ln{e} \approx \ln{2,7}$ ergibt sich $u^{*}=u(2,7 z)\cdot \kappa$ . Eine ausführliche Herleitung ist in [Etling2008] zu finden.

[11]	‘Vorticity’ ist das englische Wort für Wirbelstärke.

[12]

Der Stokes’sche Integralsatz besagt, dass sich innerhalb einer geschlossenen Fläche $\mathcal{A}$ enstehende Wirbel eines Vektorfeldes $\vec{F}$ zu einer Gesamtzirkulation entlang der Umrandung $\mathcal{C}(\mathcal{A})$ addieren (vgl. [Bronstein2001]):

$\oint\limits_{\mathcal{C}(\mathcal{A})}^{} \vec{F} \cdot \rm{d}\vec{r} = \int\limits_{\mathcal{A}}^{} \vec{\nabla} \times \vec{F} \cdot \rm{d}\vec{A}$

[13]	Am Äquator wechselt der Coriolis-Parameter das Vorzeichen. Anstelle zu Kreisbewegungen kommt es hier zu wellenartigen Trägheitsbewegungen um den Äquatorgürtel.

[14]	Bei einem Erdumfang in dieser Breitenlage (60° N) von ca. 20000 km treten somit zwei bis maximal drei Tröge bzw. Keile auf (Wellenzahl 2-3).

[15]	World-Weather-Watch-System (WWW), auch als ‘Global-Observation- System’ (GOS) bezeichnet

[16]	European Centre for Medium Range Weather Forecatsts, ECMWF

[17]	T steht hierbei für “truncation” = Abschnitt

Literaturhinweise:

[BMWI2008]

(1, 2) Bundesministerium für Wirtschaft (BMWI): Energiedaten – nationale und internationale Entwicklung. 2008, http://bmwi.de/BMWi/Navigation/Energie/statistik-und-prognosen.html

[Balzer1998]

(1, 2, 3, 4, 5, 6, 7) Konrad Balzer, Wolfgang Enke und Werner Wehry: Wettervorhersage – Mensch und Computer, Daten und Modelle. Springer-Verlag, 1998.

[Boljahn2009]

(1, 2, 3) Marcus Boljahn: Rossby-Wellen. Instituts für Meteorologie, FU Berlin, 2009. http://wekuw.met.fu-berlin.de/protu/ROSSBY-Wellen.html

[Bronstein2001]

I.N. Bronstein, K.A. Semendjajev, G.Musiol und H. Muhlig: Taschenbuch der Mathematik. Harri Deutsch Verlag, Frankfurt am Main, 2001.

[Etling2008]

(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13) Dieter Etling. Theoretische Meteorologie. Springer-Verlag, Berlin, 2008.

[EZMWF2007]

(1, 2, 3) Europäisches Zentrum für mittelfristige Wettervorhersage (EZMWF): Offizielle Broschüre, 2007.

[Hupf2005]

(1, 2, 3, 4, 5, 6) Peter Hupfer und Wilhem Kuttler: Witterung und Klima. Teubner-Verlag, Wiesbaden, 2005.

[Klose2008]

(1, 2, 3, 4, 5, 6, 7) Brigitte Klose: Meteorologie. Springer-Verlag, 2008.

[Kuchling2004]

Horst Kuchling: Taschenbuch der Physik. Fachbuchverlag Leipzig im Carl Hanser Verlag, München, 2004.

[Kunz2006]

(1, 2) Michael Kunz, Christian Hauck und Christoph Kottmeier: Skript Meteorologische Naturgefahren. Institut fur Meteorologie und Klimaforschung, Universität Karlsruhe, 2006.

[Malberg2007]

(1, 2, 3) Horst Malberg: Meteorologie und Klimatologie. Springer-Verlag, Berlin, 2007.

[Pichler1986]

(1, 2, 3, 4, 5, 6, 7, 8) Helmut Pichler: Dynamik der Atmosphäre. Bibliographisches Institut, Mannheim / Zürich, 1986.