Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.11: The Function log(z)

Last updated

May 3, 2023
Save as PDF
- 1.10: Concise summary of branches and branch cuts
- 1.12: Inverse Euler formula

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Our goal in this section is to define the log function. We want $\text{log} (z)$ to be the inverse of $e^z$ . That is, we want $e^{\text{log} (z)} = z$ . We will see that $\text{log} (z)$ is multiple-valued, so when we use it we will have to specify a branch.

We start by looking at the simplest example which illustrates that $\text{log} (z)$ is multiple-valued.

Example $\PageIndex{1}$

Find $\text{log} (1)$ .

Solution

We know that $e^{0} = 1$ , so $\text{log} (1) = 0$ is one answer.

We also know that $e^{2\pi i} = 1$ , so $\text{log} (1) = 2\pi i$ is another possible answer. In fact, we can choose any multiple of $2\pi i$ :

$\text{log} (1) = 2n \pi i \nonumber$

where $n$ is any integer.

This example leads us to consider the polar form for $z$ as we try to define $\text{log} (z)$ . If $z = re^{i \theta}$ then one possible value for $\text{log} (z)$ is

$\begin{align*} \text{log} (z) &= \text{log} (re^{i \theta}) \\[4pt] &= \text{log} (r) + i \theta, \end{align*}$

here $\text{log} (r)$ is the usual logarithm of a real positive number. For completeness we show explicitly that with this definition $e^{\text{log} (z)} = z$ :

$\begin{align*} e^{\text{log} (z)} &= e^{\text{log} (r) + i \theta} \\[4pt] &= e^{\text{log} (r)} e^{i \theta} \\[4pt] &= re^{i \theta} \\[4pt] &= z \end{align*}$

Since $r = |z|$ and $\theta = \text{arg} (z)$ we have arrived at our definition.

Definition: Complex Log Function

The function $\text{log} (z)$ is defined as

$\text{log} (z) = \text{log} (|z|) + i \text{arg} (z), \nonumber$

where $\text{log} (|z|)$ is the usual natural logarithm of a positive real number.

Remarks.

Since $\text{arg} (z)$ has infinitely many possible values, so does $\text{log} (z)$ .
$\text{log} (0)$ is not defined. (Both because $\text{arg} (0)$ is not defined and $\text{log} (|0|)$ is not defined.)
Choosing a branch for $\text{arg} (z)$ makes $\text{log} (z)$ single valued. The usual terminology is to say we have chosen a branch of the log function.
The principal branch of log comes from the principal branch of arg. That is,

$\text{log} (z) = \text{log} (|z|) + i \text{arg} (z)$ , where $-\pi < \text{arg} (z) \le \pi$ (principal branch).

Example $\PageIndex{2}$

Compute all the values of $\text{log} (i)$ . Specify which one comes from the principal branch.

Solution

We have that $|i| = 1$ and $\text{arg} (i) = \dfrac{\pi}{2} + 2n \pi$ , so

$\begin{align*} \text{log} (i) &= \text{log} (1) + i \dfrac{\pi}{2} + i 2n \pi \\[4pt] &= i \dfrac{\pi}{2} + i2n\pi, \end{align*}$

where $n$ is any integer.

The principal branch of $\text{arg} (z)$ is between $-\pi$ and $\pi$ , so $\text{Arg} (i) = \pi /2$ . Therefore, the value of $\text{log} (i)$ from the principal branch is $i \pi /2$ .

Example $\PageIndex{3}$

Compute all the values of $\text{log} (-1 - \sqrt{3} i)$ . Specify which one comes from the principal branch.

Solution

Let $z = -1 - \sqrt{3} i$ . Then $|z| = 2$ and in the principal branch $\text{Arg} (z) = -2\pi /3$ . So all the values of $\text{log} (z)$ are

$\text{log} (z) = \text{log} (2) - i \dfrac{2\pi}{3} + i2n \pi. \nonumber$

The value from the principal branch is $\text{log} (z) = \text{log} (2) - i 2\pi /3$ .

Figures showing $w = \text{log} (z)$ as a mapping

The figures below show different aspects of the mapping given by $\text{log}(z)$ .

In the first figure we see that a point $z$ is mapped to (infinitely) many values of $w$ . In this case we show $\text{log} (1)$ (blue dots), $\text{log} (4)$ (red dots), $\text{log} (i)$ (blue cross), and $\text{log} (4i)$ (red cross). The values in the principal branch are inside the shaded region in the $w$ -plane. Note that the values of $\text{log}(z)$ for a given $z$ are placed at intervals of $2\pi i$ in the $w$ -plane.

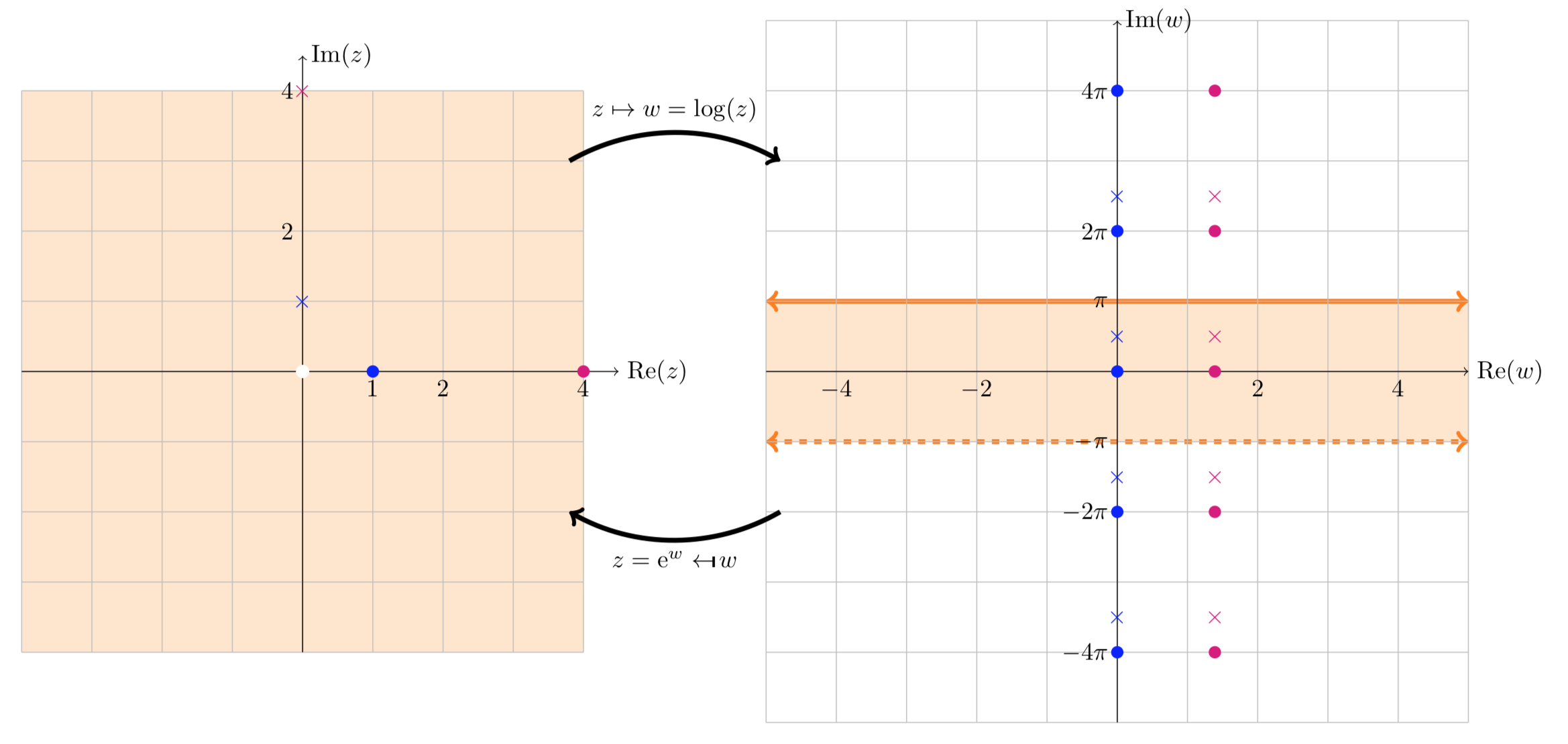
$屏幕快照 2020-09-02 下午1.36.30.png$
Mapping $\text{log} (z): \text{log} (1), \text{log} (4), \text{log} (i), \text{log} (4i)$

The next figure illustrates that the principal branch of log maps the punctured plane to the horizontal strip $-\pi < \text{Im} (w) \le \pi$ . We again show the values of $\text{log} (1), \text{log} (4), \text{log} (i), \text{log} (4i)$ . Since we’ve chosen a branch, there is only one value shown for each log.

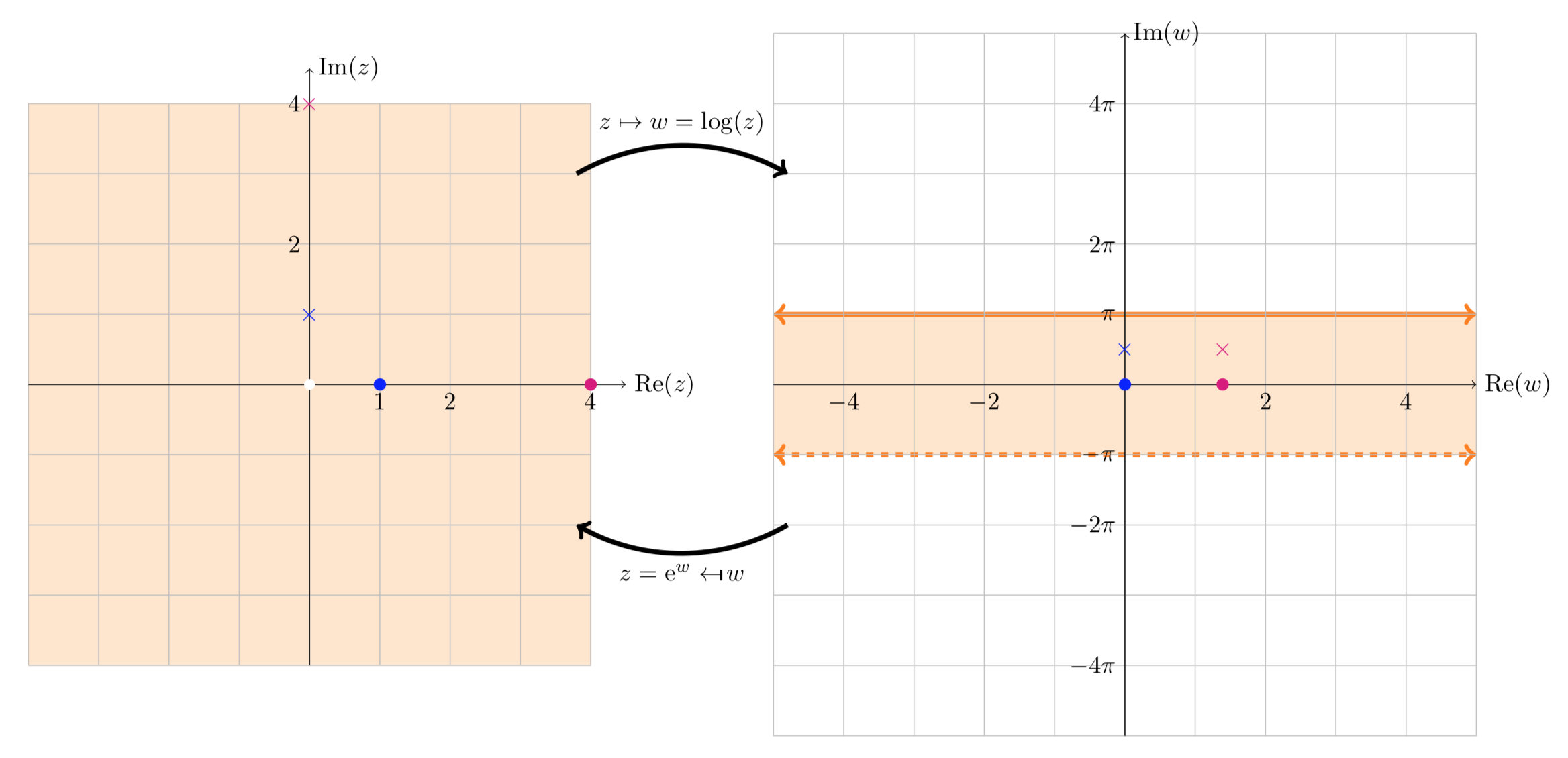
$屏幕快照 2020-09-02 下午1.43.26.png$
Mapping $\text{log} (z)$ : the principal branch and the punctured plane

The third figure shows how circles centered on 0 are mapped to vertical lines, and rays from the origin are mapped to horizontal lines. If we restrict ourselves to the principal branch the circles are mapped to vertical line segments and rays to a single horizontal line in the principal (shaded) region of the $w$ -plane.

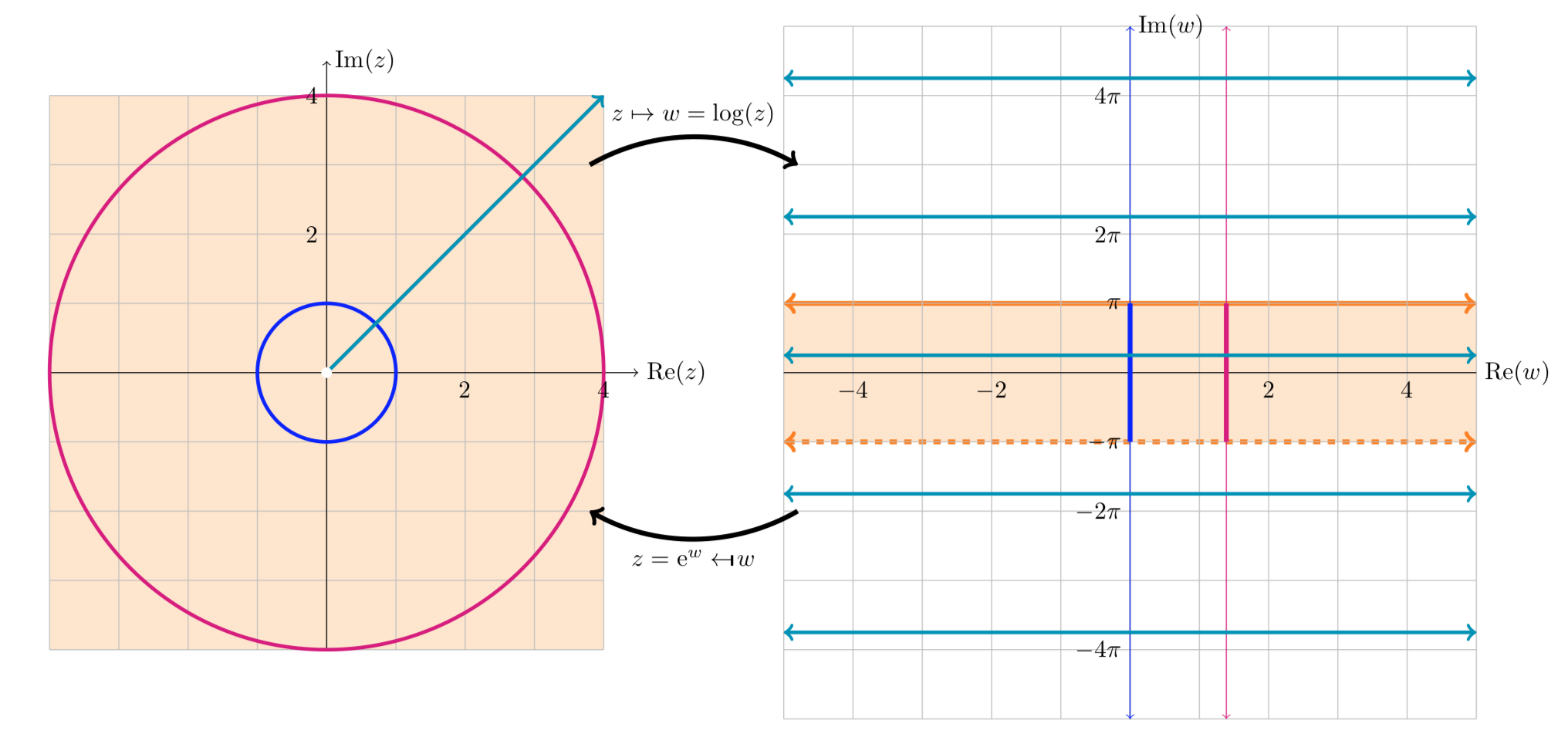
$屏幕快照 2020-09-02 下午1.46.29.png$
Mapping $\text{log} (z)$ : mapping circles and rays

Complex Powers

We can use the log function to define complex powers.

Definition: Complex Power

Let $z$ and $a$ be complex numbers then the power $z^{a}$ is defined as

$z^a = e^{a \text{log} (z)}. \nonumber$

This is generally multiple-valued, so to specify a single value requires choosing a branch of $\text{log} (z)$ .

Example $\PageIndex{4}$

Compute all the values of $\sqrt{2i}$ . Give the value associated to the principal branch of $\text{log} (z)$ .

Solution

We have

$\text{log} (2i) = \text{log} (2e^{\dfrac{i \pi}{2}}) = \text{log} (2) + i \dfrac{\pi} {2} + i2n \pi. \nonumber$

So,

$\begin{align*} \sqrt{2i} &= (2i)^{1/2} \\[4pt] &= e^{\frac{\text{log} (2i)}{2}} \\[4pt] &= e^{\frac{\text{log} (2)}{2} + \dfrac{i\pi}{4} + in \pi} \\[4pt] &= \sqrt{2} e^{\dfrac{i\pi}{4} + in\pi}. \end{align*}$

(As usual $n$ is an integer.) As we saw earlier, this only gives two distinct values. The principal branch has $\text{Arg} (2i) = \pi /2$ , so

$\begin{align*} \sqrt{2i} &= \sqrt{2} e^{(\frac{i \pi }{4})} \\[4pt] &= \sqrt{2} \frac{(1 + i)}{\sqrt{2}} \\[4pt] &= 1 + i. \end{align*}$

The other distinct value is when $n = 1$ and gives minus the value just above.

Example $\PageIndex{5}$

Cube roots: Compute all the cube roots of $i$ . Give the value which comes from the principal branch of $\text{log} (z)$ .

Solution

We have $\text{log} (i) = i \dfrac{\pi}{2} + i 2n \pi$ , where $n$ is any integer. So,

$i^{1/3} = e^{\frac{\text{log} (i)}{3}} = e^{i \frac{\pi}{6} + i \frac{2n \pi}{3}}$

This gives only three distinct values

$e^{i\pi /6}, e^{i5\pi /6}, e^{i9\pi /6}$

On the principal branch $\text{log} (i) = i \dfrac{\pi}{2}$ , so the value of $i^{1/3}$ which comes from this is

$e^{i\pi /6} = \dfrac{\sqrt{3}}{2} + \dfrac{i}{2}$ .

Example $\PageIndex{6}$

Compute all the values of $1^{i}$ . What is the value from the principal branch?

Solution

This is similar to the problems above. $\text{log} (1) = 2n\pi i$ , so

$1^{i} = e^{i \text{log} (1)} = e^{i2n\pi i} = e^{-2n\pi}, \nonumber$

where $n$ is an integer.

The principal branch has $\text{log} (1) = 0$ so $1^i = 1$ .

Example 1.11.1\PageIndex{1}

Solution

Definition: Complex Log Function

Example 1.11.2\PageIndex{2}

Solution

Example 1.11.3\PageIndex{3}

Solution

Figures showing w=log(z)w = \text{log} (z) as a mapping

Complex Powers

Definition: Complex Power

Example 1.11.4\PageIndex{4}

Solution

Example 1.11.5\PageIndex{5}

Solution

Example 1.11.6\PageIndex{6}

Solution

Support Center

How can we help?

Example $\PageIndex{1}$

Example $\PageIndex{2}$

Example $\PageIndex{3}$

Figures showing $w = \text{log} (z)$ as a mapping

Example $\PageIndex{4}$

Example $\PageIndex{5}$

Example $\PageIndex{6}$