Signs (or how to annoy a symplectic topologist)

Posted on 2015-08-23 by Chris Wendl

In this post, I will finally address that most pressing question of our times:

For ****’s sake, is it $\omega(X_H,\cdot) = dH$ or $\omega(X_H,\cdot) = -dH$ ?

My original motivation to write this post was actually a slightly different sign question, which I hadn’t realized until recently is quite closely related to this one. If you’ve seen me at any conferences recently, you may already be able to guess what I’m referring to, because I’ve developed a habit of interrupting other people’s talks to make the following seemingly frivolous observation:

The symplectization of $M$ is ${\mathbb R} \times M$ , not $M \times {\mathbb R}$ .

I don’t mean to sound dogmatic, and I don’t bring up this point just to annoy people — I bring it up because most people don’t realize there is an issue here that goes beyond a matter of arbitrary convention, and as anyone who’s ever tried to understand Floer-type theories with something other than ${\mathbb Z}_2$ -coefficients will tell you, being careless with orientations can easily lead to trouble. This kind of trouble:

Still with me? Good.

So is it R times M or M times R?

The issue with the symplectization of a contact manifold is very simple. In the literature it appears most often in the following form: assume $(M,\xi)$ is a contact manifold with contact form $\alpha$ . The symplectization of $(M,\xi)$ can then be described as a manifold diffeomorphic to ${\mathbb R} \times M$ with an exact symplectic form $\omega = d(e^t\alpha)$ ; or sometimes one presents the symplectization instead as $(0,\infty) \times M$ with $\omega = d(t\alpha)$ , which is fine since these two constructions are obviously symplectomorphic. What is not fine, but is nonetheless often done in papers by quite prominent authors (including the paper that gave this blog its name), is to write $\omega$ in one of the above forms but write the manifold itself as $M \times {\mathbb R}$ or $M \times (0,\infty)$ . Why isn’t this fine? Well, I assume we can all agree on the following:

If $X$ and $Y$ are two oriented manifolds, then $X \times Y$ inherits a canonical orientation, with a positively oriented local coordinate system given by $(x_1,\ldots,x_m,y_1,\ldots,y_n)$ for any choice of positively oriented local coordinates $(x_1,\ldots,x_m)$ on $X$ and $(y_1,\ldots,y_n)$ on $Y$ .
Any symplectic manifold $(W,\omega)$ carries a canonical orientation, namely the one defined by the volume form $\omega \wedge \ldots \wedge \omega$ .
Any contact manifold $(M,\xi)$ with a co-oriented contact structure also carries a canonical orientation, namely the one defined by $\alpha \wedge d\alpha \wedge \ldots \wedge d\alpha$ for any choice of contact form $\alpha$ compatible with the co-orientation of $\xi$ .

The second point is the reason why, for example, it’s important in symplectic topology to make the distinction between ${\mathbb C} P^2$ (carrying its natural orientation as a complex manifold) and $\overline{{\mathbb C} P}^2$ , the same manifold with reversed orientation. The first admits a symplectic structure but the second does not, since we know from de Rham cohomology that there is no closed 2-form $\omega$ on $\overline{{\mathbb C} P}^2$ satisfying $\omega \wedge \omega > 0$ .

Similarly, if $(M,\xi)$ is a co-oriented contact manifold, then $M$ inherits a canonical orientation and therefore so does ${\mathbb R} \times M$ — and it is easy to check that the latter matches the canonical orientation determined by the symplectic form $d(e^t\alpha)$ . But since ${\mathbb R}$ and $M$ are both odd-dimensional, $M \times {\mathbb R}$ has the opposite orientation. The wrong one. There is no arbitrary convention involved.

How well do you know the cotangent bundle, really?

If I were really so dogmatic, I would tell you that that’s the end of the story, but of course it isn’t. I did make one choice in the above discussion: I chose to write the symplectic form on the symplectization as $d(e^t\alpha)$ or $d(t\alpha)$ . These two conventions are indeed equivalent, and up to the choice of writing the ${\mathbb R}$ -coordinate as $t$ and the contact form as $\alpha$ , every paper I’m aware of in the symplectic/contact literature follows one of these two conventions. (Please feel free to point out exceptions in the comments, if you know any!) However, these are not the only two conventions that might conceivably make sense: one could reasonably choose to write the symplectic form differently, and depending on this choice, one might be forced to write $M \times {\mathbb R}$ instead of ${\mathbb R} \times M$ . Let me explain.

We need to recall quickly why the symplectization of $(M,\xi)$ — despite appearances to the contrary in the formula $\omega = d(e^t\alpha)$ — doesn’t actually depend on the choice of contact form. The canonical definition of the symplectization is as a particular symplectic submanifold of $T^*M$ , namely

$S_\xi M \subset T^*M$

is the submanifold consisting of all $\lambda \in T^*M$ such that $\lambda|_\xi = 0$ and $\lambda > 0$ in the direction positively transverse to $\xi$ . In other words, $S_\xi M$ is a fiber bundle over $M$ whose sections are precisely the contact forms for $\xi$ . A choice of contact form $\alpha$ trivializes this fiber bundle and defines a diffeomorphism

${\mathbb R} \times M \to S_\xi M : (t,q) \mapsto e^t \alpha_q$ ,

such that the canonical 1-form on $T^*M$ pulls back to ${\mathbb R} \times M$ as $e^t \alpha$ . The contact condition for $\xi$ thus turns out to be equivalent to the condition that $S_\xi M$ is a symplectic submanifold of $T^*M$ , and according to a standard convention, the above diffeomorphism identifies $S_\xi M$ with $({\mathbb R} \times M,d(e^t\alpha))$ .

Wait, wait… did you say “convention”?

Yes, there was exactly one semi-arbitrary convention involved in what I just said. Did you see it? I’ll give you a moment. Once you’re ready for the answer, scroll past this video of a dog lamenting the horrors of sign errors:

So here’s the thing:

The symplectic form on $T^*M$ is not canonical.

Cotangent bundles do of course have canonical Liouville forms. As we all learned in Symplectic Geometry 101, there is a 1-form $\lambda_{\text{can}}$ defined on $T^*M$ such that if you choose any local coordinates $(q_1,\ldots,q_n)$ on a neighborhood in $M$ and let $(p_1,\ldots,p_n)$ denote the induced coordinates on the fibers over that neighborhood, then

$\lambda_{\text{can}} = \sum_{j=1}^n p_j \, d q_j$ .

Since it’s obvious from the formula that $d\lambda_{\text{can}}$ is symplectic, we often assume that $d\lambda_{\text{can}}$ is the “canonical” symplectic form on $T^*M$ . By why should it be? Why shouldn’t the symplectic form be $-d\lambda_{\text{can}}$ ?

If this strikes you as a silly question, keep reading.

(Update 24/08/2015: Patrick Massot makes a very good point below in the comments, that “canonical” is perhaps the wrong word to be using here — $\lambda_{\text{can}}$ can more accurately be called a tautological 1-form, and $d\lambda_{\text{can}}$ can just as accurately be called a “tautological 2-form” on $T^*M$ . This reinforces my opinion that $d\lambda_{\text{can}}$ is the “best” choice for a symplectic form on $T^*M$ , though it is not the only reasonable choice.)

What, you haven’t asked Isaac Newton’s opinion?

One could argue in various ways that $d\lambda_{\text{can}}$ and $-d\lambda_{\text{can}}$ are equally good choices of symplectic forms on $T^*M$ ; for instance, the canonical Liouville vector field (pointing outward in the fibers) is Liouville with respect to both of them. In fact, there are situations in which one must take $-d\lambda_{\text{can}}$ instead of $d\lambda_{\text{can}}$ . This leads us back to the question that started this post, the question that has caused countless headaches to graduate students attempting to start their first research projects in Floer homology and related subjects:

I ask you for the last ****ing time, is it $\omega(X_H,\cdot) = dH$ or $\omega(X_H,\cdot) = -dH$ ?

The symplectic literature is pretty evenly split in its opinion about the definition of a Hamiltonian vector field, but there’s a basic rule of thumb that I would say must always be (and usually is) observed. Whatever sign conventions you choose, they must lead to a version of Hamilton’s equations that physicists would recognize.

An undergraduate physics student would write Hamilton’s equations as follows:

$\displaystyle \dot{q}_j = \frac{\partial H}{\partial p_j},$ $\displaystyle \dot{p}_j = - \frac{\partial H}{\partial q_j}$ ,

where $q_1,\ldots,q_n$ are the “position” variables (moving in $M$ ) and $p_1,\ldots,p_n$ are the “momentum” variables (moving in the fibers of $T^*M$ ). In the special case where $M = {\mathbb R}^n$ and we’re talking about motion in a Newtonian potential, that same physics student will define $H$ by

$\displaystyle H(q,p) = \sum_{j=1}^n \frac{p_j^2}{2 m_j} + V(q)$ ,

where $V(q)$ is the potential energy, and the positive term in front of it (depending on some constant masses $m_1,\ldots,m_n > 0$ ) is the kinetic energy. To make sure you’ve gotten the signs right in Hamilton’s equations, all you have to do is plug in this formula and compute $\dot{q}_j = p_j / m_j$ , which is really what $\dot{q}_j$ had better be if you’re going to refer to $p_1,\ldots,p_n$ as “momentum” variables. If you end up defining momentum as minus mass times velocity, then you’ve clearly done something wrong.

So if you accept what I’ve just said, then it forces upon us the following dichotomy:

Option 1: You can define Hamiltonian vector fields by $\omega(X_H,\cdot) = -dH$ , and then you get the correct local version of Hamilton’s equations if the symplectic structure on $T^*M$ is

$\omega = d\lambda_{\text{can}} = \sum_{j=1}^n d p_j \wedge d q_j$ .

In this case, the symplectization of $(M,\xi)$ can be written as $({\mathbb R} \times M,d(e^t\alpha))$ , but not as $M \times {\mathbb R}$ since the latter has the wrong orientation.

Option 2: If you prefer to write $\omega(X_H,\cdot) = dH$ , then you get the correct local expression for Hamilton’s equations if the symplectic structure on $T^*M$ is

$\omega = - d\lambda_{\text{can}} = \sum_{j=1}^n d q_j \wedge d p_j$ .

I have seen papers that conform to this convention, but most of them either don’t deal at all with contact geometry, or they do so but get some of the orientations wrong. Assuming $\dim M = 2n-1$ , one would have to write the symplectization of $(M,\xi)$ in this case as

$({\mathbb R} \times M, - d(e^t\alpha))$ if $n$ is even,

$(M \times {\mathbb R}, - d(e^t\alpha))$ if $n$ is odd.

For reasons that should by now be obvious, I prefer the first option. I have never seen the second option implemented in a consistent way in any paper; if I did, I would certainly find it a bit perverse, but I could not call it wrong.

(Acknowledgement: Thanks to Yankı Lekili for a conversation that helped me greatly in getting my thoughts on this topic in order. The correct order, not the wrong order.)

About Chris Wendl

I'm a professor of mathematics at Humboldt University in Berlin. My research deals with symplectic manifolds, contact manifolds, pseudoholomorphic curves and various related things.

View all posts by Chris Wendl →

This entry was posted in Uncategorized and tagged foundations, SFT. Bookmark the permalink.

13 Responses to Signs (or how to annoy a symplectic topologist)

Paolo says:

2015-08-23 at 22:10

There is a sign mistake in either of the last two formulas (which is, by the way, a correct plural form of “formula” in Latin: the accusative instead of the nominative “formulae”) but I’m too lazy to figure out where,

Kronheimer and Mrowka in “Monopoles and contact structures” use $\frac 12 d(t^2 \alpha)$ for the symplectisation.

LikeLike

Reply
- Chris Wendl says:
  
  2015-08-23 at 22:38
  
  I don’t see a sign error. (And if you’re applying Latin declensions to your sentence, shouldn’t it be the genitive?)
  
  Thanks for the Kronheimer-Mrowka tip, I hadn’t seen that before. Thankfully, their orientations appear to be correct.
  
  LikeLike
  
  Reply
  - Paolo says:
    
    2016-01-17 at 23:03
    
    Now I don’t see a sign mistake anymore; maybe I didn’t notice you inverted the order of $\mathbb{R}$ and $M$ . And yes, genitive should be the case to use, but I was not applying Latin declensions in an English sentence; that would be wrong and silly. I was arguing in favour of “formulas” as a legitimate plural of “formula”.
    
    LikeLike
    
    Reply
Patrick says:

2015-08-24 at 11:50

I think the reason why people laugh at this debate is because we never heard of any statement or proof which turned out to be wrong because of this orientation issue (here I exclude any “mistake” that you can correct simply by reordering $M \times \mathbb{R}$ into $\mathbb{R} \times M$ ).

About the core debate: what do you mean by “The symplectic form on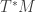 $T^*M$ is not canonical”? As far as I know there are two (non-exclusive) usual well defined meanings to the word canonical: one related to functoriality and one related to universal or tautological properties.

Here functoriality certainly imposes that any diffeomorphism of $M$ should lift to a symplectomorphism of 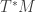$T^*M$ . This pins down $\omega_{can}$ only up to multiplication by a non-zero constant. So it doesn’t help to settle the sign issue.

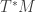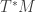Tautology does help. The canonical symplectic structure on $T^*M$ is characterized by its tautological property: for any 1-form $\alpha$ we have $\alpha^*\omega_{can} = d\alpha$ where, on the left-hand side, we only think of $\alpha$ as a smooth map from $M$ to $T^*M$ . This property is not enjoyed by $-\omega_{can}$ unless you are ready to change the sign of Cartan’s exterior derivative.

Now let’s contemplate a bit of wisdom from the old masters: in Mathematical methods of classical mechanics, Arnold defines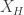 $X_H$ by $dH = \omega(\cdot, X_H)$ . Of course the down side is that you cannot use the usual interior product. But what Arnold really does is smarter. 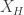The definition of a symplectic form fixes a sign and a notation for the isomorphism between $V$ and $V^*$ given a non-degenerate bilinear form on a vector space $V$ and then uses it to define $X_H$ , emphasizing the role of non-degeneracy.

LikeLiked by 1 person

Reply
- Chris Wendl says:
  
  2015-08-24 at 22:49
  
  I find this point about the tautological property of $d\lambda_{\text{can}}$ fairly convincing and have added a paragraph about it to the main text of the post.
  
  LikeLike
  
  Reply
Janko says:

2015-08-24 at 17:48

I know of one source which (will) define(s) the symplectic form on the symplectization as $-d(e^t\alpha)$ (I can’t wait for Paolo’s comments on the grammar of this sentence): It’s the forthcoming new edition of McDuff/Salamon’s “Intro to Symplectic Topology”.
They are forced to use $\omega_{\rm can}=-d\lambda_{\rm can}$ on cotangent bundles by their desire to reconcile two other seemingly “obvious” conventions: People talking about (almost) complex geometry routinely write the symplectic form on $\mathbb R^{2n}$ as $\omega_{\rm can}=\sum dx_j \wedge dy_j$ , whereas when you talk about mechanics you would write it, as Chris did, $\omega_{\rm can} = \sum dp_j \wedge dq_j$ . The problem here is that in the interpretation of $\mathbb R^{2n}$ as $T^*\mathbb R^n$ you would typically think of the $x$ -plane as the base, and the $y$ -planes as the fibers, so you would want to identify $x$ with $q$ and $y$ with $p$ …

LikeLike

Reply
- Chris Wendl says:
  
  2015-08-24 at 18:37
  
  That’s wild. I’ve noticed this issue about complex geometry before and have dealt with it slightly differently. In my 2010 paper “Strongly fillable contact manifolds and J-holomorphic foliations” (the one that classifies the fillings of $T^3$ ), in section 5, I used coordinates $(q_1,q_2,p_1,p_2)$ on $T^*T^2$ and identified it with the product of two Riemann cylinders such that the complex structure maps $\partial_{p_j}$ to $\partial_{q_j}$ , rather than the other way around. I vaguely recall getting myself quite confused before deciding that that particular convention seemed like the lesser of all available evils.
  
  So I guess for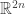 ${\mathbb R}^{2n}$ , my approach would be to set $x=p$ and $y=q$ . Because why not?
  
  LikeLike
  
  Reply
  - Janko says:
    
    2015-08-24 at 19:25
    
    You sometimes find Hamilton’s equations written out with $x=q$ and $y=p$ , I have not yet seen them the other way round…
    
    LikeLike
    
    Reply
    - Chris Wendl says:
      
      2015-08-24 at 21:22
      
      That’s a detail I’ve never paid any attention to, so I’ll take your word for it. I always just figure that calling the variables $x$ and $y$ takes away their physical meaning, so then it doesn’t matter.
      
      LikeLike
      
      Reply
- floerhomology says:
  
  2015-08-24 at 19:48
  
  No, please don’t change the sign of the symplectic form on the symplectization. That would make me very sad. 😦
  
  LikeLike
  
  Reply
  - Janko says:
    
    2015-08-25 at 16:18
    
    I suppose you’d have to petition Dietmar to make your case. I have no idea what the schedule for getting the new version to the printers is…
    
    LikeLike
    
    Reply
    - Patrick Massot says:
      
      2015-08-25 at 21:19
      
      For what it’s worth, I also vote for keeping the correct symplectic form on the cotangent bundle and on symplectizations. This book is a rather important reference in the field and I think it would harm a lot of newcomers to be exposed to this heresy.
      
      LikeLike
      
      Reply
Alex Shpilkin says:

2019-01-06 at 19:13

I feel like I should point out that the weird dimension-dependent symplectization in Option 2 doesn’t appear if you agree to orient contact manifolds as $(-\alpha)\wedge d(-\alpha)\wedge\cdots\wedge d(-\alpha)$ .

… Trivial, but maybe of some use when you want to stick with $dq\wedge dp$ . For example, if I want to also view the phase space $\mathbf R^2 =\{q,p\}$ also as the complexification $\mathbf C =\{q+ip\}$ of the configuration space $\mathbf R =\{q\}$ , it appears exceedingly weird to have the volume form on $\mathbf C$ be $dp\wedge dq$ rather than the opposite.

[Sorry, didn’t understand the math syntax at first. Delete my previous comment, please.]

LikeLike

Reply