MASSIMILIANO BADINO*
And Yet It Stands: The Stability of the Solar System in Eighteenth Cen-
tury Physical Astronomy
ABSTRACT
The proof of the stability of the solar system has been customarily presented as the solution of a great
riddle originated by Newton and completed by Laplace. In this paper, I held a different narrative. I
argue that Newton considered the stability of the solar system more a theological problem than a
physical and that he never raised the question whether the system is stable or unstable. After the
introduction of analytical techniques, astronomers and mathematicians, concerned especially with
practical problems such as the behavior of the Moon and with the improvement of perturbation theory,
also largely neglected the issue of stability. It was only in 1781, when the cultural and scientific
conditions were ripe that Lagrange, not Laplace, finally set and solved, according to the standard of
the time, the stability problem.
KEYWORDS: Physical Astronomy, Lagrange, Laplace, Stability of the Solar System, Mechanics,
Natural Philosophy
*
The following abbreviations are used: EOO, Leonhard Euler Opera Omnia, Series II (Zürich: Füssli, 1912);
GHA, The General History of Astronomy: Planetary Astronomy from the Renaissance to the Rise of Astrophys-
ics. Part B: The Eighteenth and Nineteenth Centuries, ed. René Taton and Curtis A. Wilson (Cambridge: Cam-
bridge University Press, 1995); MARS, Mémoires de l’Academie Royale des Sciences; OLG, Œuvres de La-
grange (Paris: Gauthier-Villars, 1867-1892); OLP, Œuvres de Laplace (Paris: Gauthier-Villars, 1878-1912).
1
�A FORGOTTEN NARRATIVE
On 2 April 1788, Pierre Simon Laplace presented at the Royal Academy of France gathered
in Paris a memoir on the secular equation of the Moon. In closing the introductory remarks,
he stated:
Thus the system of the world only oscillates around a mean state from which it never departs
except by a very small quantity. By virtue of its constitution and the law of gravity, it enjoys a
stability that can be destroyed only by foreign causes […]. This stability of the system of the
world, which assures its duration, is one of the most remarkable among all phenomena, in that
it exhibits in the heavens the same intention to maintain order in the universe that nature has
so admirably observed on earth for the sake of preserving individuals and perpetuating species.1
In hindsight, this passage is doubly ironic. Firstly, in little more than one year the French
Revolution would wipe out the social and political order that Laplace saw as essential for the
preservation of human species. Secondly, barely seven years previously, “one of the most
remarkable among all phenomena,” i.e., the stability of the solar system, was not even an
object of scientific inquiry.
Very few episodes in the history of science enjoy a narrative as straightforward and well-
established as the proof of the stability of the solar system. The story goes that, as a direct
1
Pierre Simon Laplace, “L’équation séculaire de la lune” (1788) OLP, XI, 243-271, on 248-249. In parenthesis,
I indicate the year in which articles were first read or presented. This year might differ considerably from the
year in which the same article was actually published.
2
�consequence of the theory of universal gravitation, Newton and his followers began wonder-
ing whether the solar system would always remain stable or, at some point, would collapse
in a spectacular series of catastrophic collisions. This problem, however, was mathematically
too difficult for Newton. The scientific world had to wait for Pierre Laplace to come to res-
cue. The French mathematician proved that the semi-major axes of the planetary orbits re-
main invariant under gravitational perturbations and that all motions in the solar system are
periodic. Sometimes it is said that this result was reached in 1773, sometimes in 1785 (or
1784, depending on the vagaries of Laplace’s bibliography), but the name of Laplace is in-
variably associated with the proof of stability.
This narrative relies on two major claims: (1) there was a problem of stability originated
by Newton’s theory and (2) Laplace solved it. Popular accounts and textbooks in celestial
mechanics subscribe this narrative almost unconditionally.2 More historically ambitious (and
more recent) works on the technical development of astronomy does not deviate substantially
from this line and also take Laplace as the hero of the stability story.3 It is interesting to note
that even an excellent historical study such as Jeff Suzuki’s, which accurately distributes
2
See, for example, Forest R. Moulton, An Introduction to Celestial Mechanics (London: MacMillan, 1914),
432 and Archie E. Roy, Orbital Motion, 2nd ed. (Bristol: IOP Publishing, 1982), 248.
3
See Victor Szebehely, Adventures in Celestial Mechanics (Austin: University of Texas Press, 1989); Ivor
Grattan-Guinness, Convolutions in French Mathematics (Basel: Birkäuser, 1990), vol. I, pp. 324-329; Florin
Diacu and Philip Holmes, Celestial Encounters. The Origins of Chaos and Stability (Princeton, NJ: Princeton
University Press, 1996); Bruno Morando, “Laplace”, GHA, 131-150; Jacques Laskar, “The Stability of the
Solar System from Laplace to the Present”, GHA, 240-248.
3
�credit between the protagonists and do not hold a Laplace-dominated narrative, still accepts
claim (1).4
Toward the end of this paper, I will come back on the reasons why this narrative has
enjoyed so much success, but for the time being, I want to discuss a different narrative, which
hinges on two new claims: (1ʹ) there was no problem of stability and (2ʹ) Lagrange solved it.
Let us spell out this apparently paradoxical pair of claims. In our present understanding, the
problem of stability of the solar system presupposes that the system can be stable or unstable
and one must decide which is the case. I claim that this physical problem did not exist in
Newton’s time. In fact, it did not exist until the moment of its solution, about 1781. For
Newton, the stability of the solar system was part of a theological, political, moral, and phil-
osophical discourse, but it was not a question to be decided by physical arguments or math-
ematical calculation. For the better part of the 18th century there was neither a stability prob-
lem nor a definition of stability with regard to which a gravitational system could be said
stable or unstable. The problem was co-created with its solution.
4
Jeff Suzuki, “A History of the Stability Problem in Celestial Mechanics from Newton to Laplace (1642-1787)”
(PhD dissertation, Boston University, 1996). One might mention even more illustrious examples, such as
Thomas Hankins in his famous Science and the Enlightenment (Cambridge, Cambridge University Press, 1985)
or the distinguished historian William McNeill in his paper "Mythistory, or Truth, Myth, History, and Histori-
ans," The American Historical Review 91, no. 1 (1986):1-10.
4
� The emergence of stability as a scientific problem is the result of two concomitant factors.
Firstly, from mid-1740s on a new analytical perturbation theory was developed, which intro-
duced several revolutionary mathematical techniques. These techniques, albeit successful,
showed some troublesome internal problems, which demanded a careful systematization.
Physical astronomy from the late 1760s to the early 1780s was driven by the necessity of
making perturbation theory more robust and reliable. This process, pursued eminently by
Lagrange, buttressed the belief that all planetary motions are strictly periodic, although their
periods can be very long. The culmination of this path was the emergence of the problem of
stability. In 1781, Lagrange showed that the lengthy analysis of the planetary motions could
in fact yields the proof that all motions are periodic.
The development of perturbation theory in the second half of the 18th century illustrates
the internal conditions that made possible to raise the question of stability and to solve it. It
does not explain, however, why the question was not raised by Newton himself, which is
precisely what the received view takes almost for granted. It is therefore essential to consider
a second factor, i.e., the profound change in the intellectual climate brought about by the
unfolding of the Enlightenment. In particular, for the emergence of the problem of stability
it is relevant the elaboration of a new conception of natural order emancipated by the tradi-
tional theological foundation. By breaking the ancient connection between theology, natural
philosophy, and other sectors of culture Enlightenment thinkers created the conditions to
raise the question about the order of the solar system as a legitimate and autonomous scien-
tific problem.
5
� In this article I focus especially on the first factor, which involves the interplay between
mathematical concepts (particularly the concept of periodicity) and mathematical practices.
This will require to pay a special attention to the concrete work of mathematicians rather than
to their scattered post facto pronunciations. The several branches of the second factor will be
the subject of a much larger study that will appear soon. Here, I merely confine myself to
sketch some key ideas concerning the larger cultural framework within which physical as-
tronomy was developed.
PROLOGUE: STABILITY IN NEWTON’S TIME
Perhaps Newton’s most famous pronouncement on the nature of the solar system—or the
system of the world as it was sometimes magniloquently called—can be found in the 31st
Query of his Opticks. Newton is surveying God’s creation and, toward the end, he stops and
examines the behavior of the heavenly bodies. He looks upon the universe as the product of
an intelligent being, who rose it from the primeval Chaos and arranged it in the order we now
observe “by the mere Laws of Nature.” Then he continues:
For while Comets move in very excentrick Orbs in all manner of Positions, blind Fate could
never make all the Planets move one and the same way in Orbs concentrick, some inconsider-
able Irregularities excepted which may have risen from the mutual Actions of Comets and
Planets upon one another, and which will be apt to increase, till the System wants a Refor-
mation.5
5
Isaac Newton, Opticks, 3rd ed. (London: William and John Innys, 1721), 378.
6
� This famous passage has been traditionally regarded as clear evidence that Newton had in
mind the problem of the stability of the solar system. He acknowledges that some irregulari-
ties in the planetary motions can accumulate until a reformatory action of God is required. In
so doing, Newton is implicitly recognizing that the solar system, if left to itself, is doomed
although “it may continue by those Laws for many Ages.” Certainly, Newton is discussing
the stability of the system, but is he really treating it as a problem? Stability is a problem
insofar as the solar system may or may not be stable, i.e., to the extent that an alternative
exists between stability and instability. One needs to formulate general conditions of stability
and to ascertain whether they apply to our solar system. In the 31st Query, Newton is con-
cerned with none of these things. On the contrary, he unequivocally says that the solar system
can and actually will change its outlook dramatically at some point. Far from raising the
question of stability, Newton is providing the answer: the solar system, qua physical system,
is not stable. In fact, Newton is not interested in the physical question of stability, rather, he
wants to make two distinct theological points: one has to do with the Millenarian issue of the
end of times and the other concerns the relation between divine and natural order. The first
point was uncontroversial. Being created by God, the universe had a beginning and will have
an end. The multiple inequalities in celestial motions support this point by showing that the
universe cannot carry on forever. Henry Pemberton, an ardent spoke-man of the Newtonian
doctrine, made precisely the same point some years later:
I think it not improper to mention a reflection made by our excellent author [Newton] upon
these small inequalities in the planets motions; which contains under it a very strong philo-
7
� sophical argument against the eternity of the world. It is thus, that these inequalities must con-
tinually increase by slow degree, till they render at length the present frame of nature unfit for
the purposes it now serves. And a more convincing proof cannot be desired against the present
constitutions having existed from eternity than this, that a certain number of years will bring it
to an end.6
This thesis on the universe’s fate was part of any good Christian’s beliefs. For astronomers
and mathematicians of faith, it was natural to link this religious truth with what they were
observing in the sky or calculated on paper. For instance, Leonhard Euler, a firm believer,
declared that the finitude of the universe was attested by the existence of the interplanetary
ether, which slows down the planets, increases their mean motions, and reduces the radii of
their orbits:
Thus, in Time the Earth ought to come within the Region of Venus, and in fine into that of
Mercury, where it would necessarily be burnt. Hence it is manifest, that the System of the
Planets cannot last for ever in its (present) State. It also incontestably follows, that this System
must have had a Beginning: For whoever denies it, must grant me, that there was a Time, when
the Earth was at the Distance of Saturn, and even farther, and consequently that no living Crea-
ture can subsist there. Nay there must have been a Time, when the Planets were nearer to some
fixt Stars than to the Sun, and in this Case they could never come into the Solar System. This
6
Henry Pemberton, A View of Sir Isaac Newton’s Philosophy (London: Palmer, 1728), 180-181. On Newton’s
cosmological views see also David Kubrin, “Newton and the Cyclical Cosmos: Providence and the Mechanical
Philosophy,” Journal of the History of Ideas 28, no. 3 (1967): 325-346 and Peter Kerszberg, “The Cosmological
Question in Newton’s Science,” Osiris 2 (1986): 69-106.
8
� then is a Proof, purely physical, that the World, in its present State, must have had a Beginning,
and must have an End.7
Moreover, any denial of the finitude of the universe would promptly lead to accusations
of Spinozism, i.e., the view according to which God coincides with Nature and both exist
necessarily. Except in radical circles, the Apocalyptic destiny of the solar system was taken
for granted.
By contrast, the second point was a bone of fierce contention. The key of the 31st Query
is the word “reformation.” For Newton, the deep significance of the imperfections of the
universe does not lie in the obvious implications for the end of times, but in the fact that they
reveal the active presence of God in nature. Newton believed that God does not confine him-
self to observing the unfolding of the natural history from afar, but organizes it according to
a pure act of will. The universe is the Dominion of a supremely intelligent, powerful, and
benevolent being and its arrangement is to be ascribed to “the counsel and contrivance of a
voluntary agent.”8 Thus, for Newton the natural cosmological order of the system of the
world depends closely on the divine order and astronomy provides arguments for voluntaris-
tic theology.
7
Letter from Leonhard Euler to the Rev. Mr. Caspar Wetstein, 28 June 1749; published partially in Philosoph-
ical Transactions 46 (1749-1750): 203-205; quotation on 204-205.
8
Newton’s first letter to Richard Bentley, 10 December 1692, in Isaac Newton’s Philosophical Writings, ed.
Andrew Janiak (Cambridge: Cambridge University Press, 2004), 95.
9
� It is important to stress that these theses of Newton were part of a longer theological tra-
dition that dated back to the thirteenth century and the work of William Ockham. According
to this tradition, later absorbed by Cambridge Platonists, the order of nature is imposed by
divine will and hence man cannot derive it from first principles and certainly cannot make it
the object of human physical science.9 Thus, the solar system is not in immediate danger of
collapse because God intervenes in the world, organizes, orders, and maintains it benevo-
lently.10 The observed inequalities disclose the long-term destiny of the universe, but they are
resources of a natural theological discourse rather than the premises of a physical question.
Samuel Clarke forcefully insisted on this point when, in his Boyle Lecture of 1705, he stated
that “[t]he preservation of the several Systems, and of the several Planets and Comets in the
9
On the relation between voluntaristic theology and the conceptions of natural order and law of nature see
Francis Oakley, “Christian Theology and the Newtonian Science: The Rise of the Concept of the Laws of Na-
ture,” Church History 30, no. 4 (1961): 433-457 and John R. Milton, “The Origin and Development of the
Concept of the Laws of Nature,” Archives Européennes de Sociologie 22 (1981): 173-195. On the influence of
medieval theology on modern science see Amos Funkenstein, Theology and the Scientific Imagination from the
Middle Ages to the Seventeenth Century (Princeton, NJ: Princeton University Press, 1986). On the concept of
natural order in the English culture, see Peter Harrison, “Laws of Nature in the Seventeenth-Century England:
From Cambridge Platonism to Newtonianism,” in The Divine Order, The Human Order, and the Order of
Nature, ed. Eric Watkins (New York: Oxford University Press, 2013), 127-148.
10
Newton insists on God’s provident maintenance of the celestial order also in the 28th Query of the Opticks
as well as in his third letter to Bentley on 11 February 1692, see Janiak, Newton’s Philosophical Writings (ref.
8), 101.
10
�same System, from falling upon each other” precisely demonstrated the existence of a su-
preme Governor.11
Two texts illustrate the implications of Newton’s voluntaristic theology in the clearest
way: the General Scholium to the second edition of the Principia (1713) and the correspond-
ence between Leibniz and Clarke (1716). Given its brevity, the amount of scholarly literature
generated by the General Scholium is stunning. This is doubtlessly due to the extreme density
of thought contained in just a few pages, which range from the nature of space and gravita-
tion, to electricity and the motion of the comets. Recent commentators, however, have espe-
cially underlined the theological project displayed by Newton in the Scholium.12 The com-
parison with contemporary heretic tracts as well as the analysis of Newton’s private writings
show clearly that he was advocating an anti-deist and unitarian theology. This theological
position also reverberates in multiple passages of the Principia.13 Newton’s voluntaristic con-
ception of God is a key element of his theological project. Nature is the dominion of God and
11
Samuel Clarke, “A Demonstration of the Being and Attributes of God: More Particularly in Answer to Mr.
Hobbs, Spinoza, and their Followers,” in The Works of Samuel Clarke, ed. John Clarke (London: John and Paul
Knapton), 513-577, quotation on 571.
12
See, for example Larry Stewart, “Seeing through the Scholium: Religion and Reading Newton in the Eight-
eenth Century,” History of Science 34 (1996): 123-165, J. E. McGuire, “The Fate and the Date: The Theology
of Newton’s Principia Revisited,” in Rethinking the Scientific Revolution, ed. Margaret J. Osler (Cambridge:
Cambridge University Press, 2000), 271-295, Stephen D. Snobelen, “God of gods, and Lord of lords. The The-
ology of Isaac Newton’s General Scholium to the Principia,” Osiris 16 (2001): 169-208.
13
See Snobelen, “God of gods” (ref. 12), 198-208.
11
�natural phenomena are the manifestation of his will. These claims are not only supposed to
counter deistic and Spinozistic views that equal God with Nature and mere necessity, but are
also the core of Newton’s empiricism and his conception of physical investigations: “We
know him by his most wise and excellent contrivances of things, and final causes; we admire
him for his perfection; […] and a God without dominion, and final causes, is nothing else but
Fate and Nature.”14 Since the universe is the product of God’s will, who proceeded by natural
laws, the understanding of the world cannot come from first principles, as Descartes and
Spinoza thought, but must derive from the painstaking investigation of nature.15
According to Newton, God rules the universe as a willful, provident, and benign designer,
who interacts with his creation when it becomes necessary.16 In November 1715, Leibniz
cautioned Caroline of Wales against this conception of God as a unskillful clockmaker who,
every now and then, is “obliged to mend his work and to set it right.”17 The letter was for-
warded to Samuel Clarke and then to Newton himself. The relation between Newton and
14
Isaac Newton, Mathematical Principles of Natural Philosophy (1729) ed. Andrew Motte and Florian Cajori,
3rd edition (Berkeley, CA: University of California Press, 1962), 546.
15
On this point see, for example, James E. Force, “Newton’s God of Dominion: The Unity of Newton’s Theo-
logical, Scientific, and Political Thought,” in Essays on the Context, Nature, and Influence of Isaac Newton’s
Theology, ed. James E. Force and Richard H. Popkin (Dordrecht: Kluwer, 1990), 75-102.
16
See Martin Tammy, “Newton, Creation, and Perception,” Isis 70 (1979): 48-58.
17
Leibniz to Caroline of Wales, November 1715, in G. W. Leibniz and Samuel Clarke – Correspondence, ed.
Roger Ariew (Indianapolis: Hackett Publishing Company, 2000), 4.
12
�Leibniz had been difficult ever since the latter’s reaction to the Principia18 and the former
did not miss the chance to fight back through Clarke. What followed was one of the most
quoted correspondence of Western philosophy. The theme of the imperfections of the system
of the world dominates the first part of the exchange and it becomes immediately clear that
the matter is eminently theological and metaphysical rather than physical. In his second letter,
Leibniz argues that, by picturing God as a clumsy clockmaker who intervenes to rewind his
imperfect creation, Newton emphasizes God’s power over his wisdom. A rational being pre-
sented with two alternatives motivates his or her course of action by a sufficient reason. In-
stead, by acting on pure will, God operates irrationally. This is enough for Leibniz to wield
the most frightening theological weapons of those times. For those insisting on God’s power
at the expenses of his wisdom undoubtedly flirt with Socinianism and “will fall exactly into
the error of the materialists and of Spinoza, from whom they profess to differ.”19
This remark hit a soft spot because, as we have seen, both Clarke and Newton did have
leanings toward Arianism and other forms of unitarian heresies. In his replies, Clarke goes
on the defensive and tries to spell out the interpretation of the 31st Query:
The word correction or amendment is to be understood, not with regard to God, but only to us.
The present frame of the solar system, for instance, according to the present laws of motion,
will in time fall into confusion and, perhaps, after that, will be amended or put into a new form.
18
See I. Bernard Cohen, Introduction to Newton’s Principia (Cambridge: Cambridge University Press, 1971),
152-156.
19
Leibniz to Clarke, end December 1715, in Correspondence (ref. 17), 9.
13
� But this amendment is only relative with regard to our conceptions. In reality, and with regard
to God, the present frame, and the consequent disorder, and the following renovation, are all
equally parts of the design framed in God’s original perfect idea.20
God’s work, Clarke claims, is not unskillful; instead, it is part of a larger and deeper plan
to “cure the disorders of nature” by actively interacting with the world and with us. Clarke
often resorts to the monarchic metaphor of God as the King of the Universe who governs the
creation by setting it in order and by “preserving and continuing the beings, powers, orders,
dispositions, and motions of all things.” The metaphor is not accidental: it characteristically
reveals the intermixture of scientific, metaphysical, theological, and political interests of this
debate.21 The discussion quickly moves to other themes, but the problem of the worldly im-
perfection resurfaces toward the end of the correspondence. In his fourth letter, Clarke states
clearly what is wrong with Leibniz’s idea that God must follow the principle of sufficient
reason:
This argument (if it is good) proves that the material world must be infinite and that it must
have been from eternity and must continue to eternity, and that God must always have created
20
Clarke to Leibniz, 10 January 1716, in Correspondence (ref. 17), 12-13.
21
As Francis Oakley has convincingly argued, the roots of this intermixture are to be sought for in the medieval
tradition of nominalistic theology see, for instance Francis Oakley, “Jacobean Political Theology: The Absolute
and Ordinary Powers of the King,” Journal for the History of Ideas 29 (1968): 323-346 and “The Absolute and
Ordained Power of God and King in the Sixteenth and Seventeenth Centuries: Philosophy, Science, Politics,
and Law,” Journal for the History of Ideas 59 (1998): 669-690.
14
� as many men and as many of all other things as it was possible for him to create and for as long
a time also as it was possible for him to do it.22
Basically, Clarke lists everything could possibly earn Leibniz an accusation of heresy:
eternity of the universe, infinity of worlds, incapability of God to act freely, and intrinsic
necessity of nature. From Clarke’s (and Newton’s) point of view, imperfections in the system
of the world are mandatory requirements to a correct (to wit, voluntaristic) theology. The
universe must have some imperfections otherwise God becomes a dispensable spectator. By
contrast, Leibniz believes that any imperfection in the system of the world undermining its
existence also undermines God’s omnipotence and omniscience.23
Thus, far from phrasing in exotic theological language a physical point about stability, in
the 31st Query Newton is doing quite the opposite: he deploys the certified physical instabil-
ity of the solar system to score a theological point about God’s presence in the world. For
Newton and his contemporaries, the imperfections of the solar system are a matter of theo-
logical discussion, not an object of physical inquiry. Not only the problem of stability never
appears in the Principia or in any other of Newton’s physical writings, but he occasionally
even downplays the role of the inequalities of the solar system. The characteristic mark of a
perturbing interaction is the precession of the aphelion of the perturbed body. However, in
22
Clarke to Leibniz, 26 June 1716, in Correspondence (ref. 17), 34.
23
See Ezio Vailati, Leibniz and Clarke: A Study of Their Correspondence (Oxford: Oxford University Press,
1997), 37-42.
15
�Book III, Proposition 14, Theorem 14, Newton claims that planetary aphelia can be consid-
ered as fixed, which is tantamount to saying that inequalities originated by mutual interac-
tions of the planets and satellites are negligible.24 Interestingly, Newton expands on same
point in the General Scholium when arguing in favor of the pervasiveness of the inverse-
square law: “[g]ravitation towards the sun is made up out of the gravitations towards the
several particles of which the body of the sun is composed; and in receding from the sun
decreases accurately as the inverse square of the distances as far as the orbit of Saturn, as
evidently appears from the quiescence of the aphelion of the planets; nay, and even to the
remotest aphelion of the comets, if those aphelions are also quiescent.”25
FIRST STEPS (AND STUMBLES) OF PERTURBATION THEORY
NEW QUESTIONS, NEW PRACTICES
The tight connection between natural and divine order had bearings both on the cultural de-
bate at large and on research in physical astronomy. As for the former, the Newtonian doc-
trine quickly became a precious resource in discussions concerning moral, philosophical, and
political reformation.26 As for the latter, the belief that the universe was the creation of a
24
Newton, Principia (ref. 14), 422.
25
Newton, Principia (ref. 14), 546, emphasis added.
26
On the role played by the Newtonian theory in moral and political debates in the late 17th century England
see Steven Shapin, “Of Gods and Kings: Natural Philosophy and Politics in the Leibniz-Clarke Disputes,” Isis
72 (1981): 187-215. Later in the 18th century, the so-called Political Newtonianism actively influenced novel
16
�benevolent God inevitably affected scientific priorities. On the one hand, the long-term sta-
bility of the solar system was not looked upon as a legitimate scientific question simply be-
cause the ultimate fate of the world was a matter of theology, not of calculation. Thus, when
Jacques Cassini, in his Elemens d’Astronomie, rhetorically asked: “can one be assured that
the orbits that the planets describe always retain the same figure and the same eccentricity,
and that they always have the same inclination with regard to one another?” he was not setting
the driving question of physical astronomy, but rather its unsurpassable limit.27 On the other
hand, the sky displayed a plethora of puzzling behaviors some of which, particularly those
related to the Lunar motion, had conspicuous practical importance, whereas others, such as
the Great Anomaly of Jupiter and Saturn, were primarily mathematical conundrums.
Newton’s analysis of these problems in the Principia relied mainly on geometrical tech-
niques. Using these meager resources, Newton was able, for example, to evaluate the per-
turbing effect of the Sun and the Earth on the Moon and to draw extraordinarily precise
quantitative descriptions of the Lunar motion. However, it was clear that, in hands less capa-
ble than his, this geometrical perturbation theory was too limited and too cumbersome to
sustain productive research in physical astronomy. Furthermore, even Newton’s genius had
not succeeded in explaining everything. Some phenomena, notably the precession of the Lu-
nar apogee, resisted Newton’s perturbation analysis, which stubbornly yielded only half of
political movements and even the constitution of the United States, see Richard Striner, “Political Newtonian-
ism: The Cosmic Model of Politics in Europe and America,” The William and Mary Quarterly 52, no. 4 (1995):
583-608.
27
Jacques Cassini, Elemens d’Astronomie (Paris: De L’Imprimerie Royale, 1740), x-xi.
17
�the observed value. Thus, shortly after Newton’s death, European mathematicians began to
think not only that physical astronomy required new and more powerful formal techniques,
but also that perhaps gravity did not provide the entire picture and had to be supplemented
by other physical hypotheses, for example the existence of an all-pervasive imponderable
fluid, whose action had to be added to planetary perturbations.
Since the early 1740s, Leonhard Euler was among the most active supporters of a program
to replace old geometrical methods with a new physical astronomy based on differential cal-
culus. Euler’s interests in astronomy date to his period at the Petersburg Academy,28 but it
was only after his move to Berlin, in 1741, that he dedicated himself systematically to this
research. In 1747, he introduced two new fundamental techniques to treat analytically the
interaction between planets that would mark the future direction of perturbation theory.29 The
central problem is laid down at the very beginning of his memoir. Since we observe preces-
sions in the planetary aphelia and lines of nodes,30 one must conclude that the solar system is
a complex web of gravitational interactions:
It is therefore very probable that, in the system of the universal gravitation, the planets are not
only attracted toward the sun, but they also attract each other by means of forces inversely
28
On Euler’s early forays in astronomy see Ronald S. Calinger, Leonhard Euler: Mathematical Genius in the
Enlightenment (Princeton, NJ: Princeton University Press, 2015).
29
Leohnard Euler, “Recherches sur le mouvement des corps cèlestes en général” (1747) EOO, II, 25, 1-44. This
paper was presented at the Berlin Academy of Science on 8 June 1747, but was published only in 1749.
30
The aphelion is the farthest point of the planetary orbit around the Sun. On the line of nodes and other orbital
elements see Figure 1.
18
� proportional to the square of the distance and the sun itself is attracted toward the planets by
similar forces.31
How to disentangle this intricate system of interwoven attractions? Euler makes clear that
the analysis of planetary perturbations requires two conditions: an accurate knowledge of the
force law and powerful computational tools to solve the resulting equations of motion. There
are legitimate doubts, however, that the first condition is fulfilled. The failure of Newton’s
theory to derive the full precession of the Lunar apogee, Euler affirms, seems to suggest that
the gravitational law needs some amendments. Interestingly, Euler also tries to show that a
modification of the force law is not incompatible with the gravitational doctrine that attrac-
tion depends inversely on the square of the distance. Newton’s theory relies on the presup-
position that the planets are perfectly homogeneous spheres, but, as a matter of fact, they are
neither perfectly spherical, nor perfectly homogeneous. Thus, Euler continues, if we imagine
that attraction is due to the interaction between individual particles, then local departures
from sphericity and homogeneity can produce a resulting force that is not exactly inverse-
square and not exactly centrally directed even though the particle-particle interaction is so.
But, cannot one infer the modifications of the gravitational law from observations? The
answer, according to Euler, is no. He believes that interplanetary space is filled up with an
31
Euler, “Le mouvement des corps” (ref. 29), 2.
19
�imponderable substance, called ether, which alters their mean motions over the century.32
Thus, one cannot use ancient observations to guess the form of the law because the presence
of the ether makes the comparison between distant observations unreliable.33
Figure 1: The motion of a planet in the space is defined by 6 orbital elements, one plane of
reference (ecliptic) one direction of reference (toward the vernal point ♈) and one time of
reference (called epoch). Two of them, eccentricity and semi-major axis, describe the shape
and size of the orbit. Two further elements determine the position of the orbital plane in the
space. For this goal, astronomers usually deploy the inclination i, which is the angle between
the orbital plane and the ecliptic, and the longitude of the ascending node Ω. The orbit inter-
sects the ecliptic in two points, one along the direction south-north, which is called the as-
cending node ☊, and one along the opposite direction (descending node). The line of nodes
is the line joining them and the longitude of the ascending node is the angle between the line
of reference and the line of nodes. Finally, two elements are needed to define the orientation
of the orbit and the position of the body. The first one is generally given by the argument of
the periapsis, i.e., the angle ω between the line of nodes and the line of the apsides between
the aphelion (A) and the perihelion (P). The second one is expressed by the true anomaly ν at
the epoch.
32
The mean motion is the angular velocity of a celestial body necessary to complete its orbit. If the ether fills
up the interplanetary space, the planetary motion is slowed down and the planet would move on a narrower
orbit with a faster mean motion.
33
Euler, “Le mouvement des corps” (ref. 29), 5-6.
20
�
This deadlock requires a reboot of the entire analysis from a more general point of view.
Euler writes the equations of motion and leaves undetermined the force. By studying cases
of increasing complexity, he tries to include the action of a resisting medium in the final
expression of the force law. However, the real breakthrough of Euler’s paper lies more in the
techniques used to manipulate the equations of motion than in the results attained. In the third
problem he sets out to calculate the motion of a body attracted by a center of force under
three assumptions: (a) the force law is only approximately proportional to the inverse square
of the distance, (b) the eccentricity of the orbit is small, and (c) they share the same plane.
The equations of motion in polar coordinates read as follows:
(1) 2𝑑𝑟𝑑𝜑 + 𝑟𝑑 & 𝜑 = 0
*+
(2) 𝑑 & 𝑟 − 𝑟𝑑𝜑 & + 𝑑𝜔& = 0
,
where a is the mean distance between Earth and Sun, Π the mean force between them, dω
the infinitesimal angle described by the Earth around the Sun, r the radius vector, 𝜑 the lon-
gitude, and V the arbitrary perturbing force. For this force, Euler gives the general expression:
0,1 2
(3) 𝑉= +𝑅
*3 4
where R is an arbitrary function of the radius vector r, while the other symbols are constants.
Euler’s method to treat this problem would set the standard approach to perturbation prob-
lems for the next thirty years. He assumes that perturbations cause a linear modification of
the unperturbed form of the coordinates r and 𝜑. In particular, if the perturbations were
21
�switched off, the body would orbit in the usual Keplerian ellipse, for which 𝑟 =
1 + 𝑒 cos 𝜈 , where e is the eccentricity and v is the eccentric anomaly.34 But as the pertur-
bations are switched on, the radius vector changes into 1 + 𝑒 cos 𝜈 + 𝑠 , where s is a small
quantity. The assumption that the action of external planets results in a slight modification of
the coordinates of the body grounds Euler’s work in perturbation theory.
By fixing the additional force term R and replacing the perturbing radius vector into the
original equations of motion, Euler finds a second-order differential equation for s in terms
of v and, to solve it, he has to guess a form of the solution. Here comes the crucial step. He
assumes that the solution has the general form:
(4) 𝑠 = 𝐴 + 𝐵 cos 𝑣 + 𝐶 cos 2𝑣 + 𝐷 cos 3𝑣
where A, B, C, and D can be calculated by the usual method of the undetermined coefficients.
In formulating s as a trigonometric series, Euler is taking a momentous step.35 Before Euler,
there was no notion of trigonometric function: sine and cosine were treated as geometrical
segments, rather than entities on which a proper calculus could be defined.36 A little earlier,
34
Euler introduced the eccentric anomaly in the previous section of the paper, see Euler, “Le mouvement des
corps” (ref. 29), 23. For this and other quantities defining the orbit see Figure 2.
35
The reason why the series is limited to three terms is probably that, after proposing an expression for R, Euler
power-expands it to the third order only.
36
See, for instance, Victor J. Katz, “The Calculus of Trigonometric Functions,” Historia Mathematica 14, no.
4 (1987): 311-324 and Louise Ahrndt Golland and Ronald W. Golland, “Euler’s Troublesome Series: An Early
Example of the Use of Trigonometric Series,” Historia Mathematica 20, no. 1 (1993): 54-67.
22
�in the same paper, Euler spends a few pages to introduce the very concept of trigonometric
series, a sign that he does not take it as commonplace knowledge.37 The use of this technique
in physical astronomy has a profound conceptual significance. But before commenting more
extensively on this point, I shall briefly discuss the second crucial innovation of Euler’s pa-
per.
Figure 2: The angles used to describe the planetary motion. The true anomaly Θ is the angle be-
tween the position of the planet on the orbit the the focus. The eccentric anomaly v is the angle be-
tween the center of the ellipse and the projection of the position of the body on the auxiliary circle.
Finally, the mean anomaly M is the angle between the center and the position the body would have
on the auxiliary circle if its motion would occur with constant velocity.
37
Euler, “Le mouvement des corps” (ref. 29), 20-21.
23
� The last problem of the article concerns the motion of a body in space under the perturba-
tion of an arbitrary force. As before, Euler writes down the equations of motion for (three)
polar coordinates, but now his main goal is to derive workable expressions for the inclination
and the longitude of the ascending node. Most probably, he has already in mind a practical
application for these formulas, i.e., the study of the Great Anomaly of Jupiter and Saturn,
which he would carry out a few months later (see below). A little geometry reveals that be-
tween the three polar coordinates r, z, 𝜑, the inclination ρ and the longitude of the ascending
node π there is the simple Keplerian relation 𝑧 = 𝑟 sin 𝜑 − 𝜋 tan 𝜚. By differentiating this
relation one arrives at:
3LM NOP QRS
(5) 𝑑𝑧 = 𝑑𝑟 sin(𝜑 − 𝜋) tan 𝜚 + 𝑟 𝑑𝜑 − 𝑑𝜋 cos 𝜑 − 𝜋 tan 𝜚 +
TUN M4
However, Euler claims that, since inclination and longitude of the node change very little
during the perturbing action, one can also derive the relation above by keeping them constant,
which yields:
(6) 𝑑𝑧 = 𝑑𝑟 sin 𝜑 − 𝜋 tan 𝜚 + 𝑟𝑑𝜑 cos 𝜑 − 𝜋 tan 𝜚
By equating (5) and (6) and using the equations of motion, Euler eliminates the coordi-
nates z, r and attains two formulas for inclination and longitude of the node in terms of the
components of the perturbing force. These formulas can be used to calculate the variation of
the orbital elements as he would show in his analysis of the Great Anomaly. This argument
is the first instance of what is today known as the method of variation of constants. From a
24
�physical point of view, Euler is supposing that the effect of the perturbing forces is to con-
tinuously modify the original ellipse. At each point of its course, the point is shifted by the
perturbing force on a new elliptic orbit—now called the osculating or intermediary orbit—
whose elements are infinitesimally changed. Consequently, the perturbed motion can be
mathematically represented as a combination of innumerable ellipses and the trajectory of
the body can be traced by a differential equation.38
The importance of trigonometric series and the method of variation of constants can hardly
be overestimated. By supposing that the solutions of the equations of motion could be for-
mulated as a combination of trigonometric functions, Euler could integrate the equations
much more easily and could use the observational data to calculate the coefficients. Further-
more, the method, although mathematically still unclear, provided a handy way to obtain
differential formulas for orbital elements from the equations of motion. But, seen in a broader
historical perspective, these computational advantages are the result of a remarkable concep-
tual turn in the way natural order is conceived.
As we have seen in the previous sections, until the late 17th, the discourse on natural order
was inextricably linked with theological reflections about the attributes of God and the divine
38
Euler would elaborate further on this method some years later in Leonhard Euler, “De motu corporum coe-
lestium a viribus quibuscunque perturbato,” (1752) EOO II, 25, 175-209. On Euler’s introduction of the method
of the variation of constants see also Curtis A. Wilson, “The Great Inequality of Jupiter and Saturn: from Kepler
to Laplace,” Archive for History of Exact Sciences 33 (1985); 15-290, especially 72-74 and Jeff Suzuki, “The
Stability Problem” (ref. 4), 122-128.
25
�order. In particular, it was customary to regard law and order in nature as aspects of a larger
issue concerning God’s omnipotence, his capability to create alternative worlds, and his pro-
pensity to perform miracles.39 God’s role as metaphysical underpinning of natural order is
still clearly visible in the founders of the mechanistic philosophy. According to Descartes,
for instance, it is God’s consistency and power that warrant natural laws such as the principle
of inertia.40 When Newton, as we have seen, wielded physical arguments to uphold his theo-
logical views against Leibniz, he was in fact following a pretty common argumentative pat-
tern relating God’s features with the innermost aspects of nature, its order and its fundamental
laws.
When theology and natural philosophy started to diverge in the early decades of the 18th
century, the conception of natural order and natural laws changed accordingly. Although the
expression ‘law of nature’ remained preferably reserved for very selected statements of par-
ticular fundamentality such as the law of inertia, one can observe a general liberalization of
the concept as signaled by the appearance of terms such as ‘laws of optics’ and even ‘laws
39
See, for instance, Funkenstein, Theology and the Scientific Imagination (ref. 9), 117-201; Francis Oakley,
Omnipotence, Covenant and Order: An Excursion in the History of Ideas from Abelard to Leibniz (Ithaca, NY:
Cornell University Press, 1984).
40
See Daniel Garber, Descartes' Metaphysical Physics (Chicago: University of Chicago Press, 1992); John
Henry, “Metaphysics and the Origins of Modern Science: Descartes and the Importance of Laws of Nature,”
Early Science and Medicine, 9, no. 2 (2004): 73-114; Walter Ott, Causation and Laws of Nature in Early Mod-
ern Philosophy (Oxford: Oxford University Press, 2009).
26
�of electric and magnetic phenomena.’41 Also the law of gravitation acquired the status of
natural law in the 1740s at the latest. When Clairaut, as we shall see below, proposed to
modify it to explain the Lunar precession, Georges Louis Leclerc de Buffon protested on the
ground that it satisfied all requisites of a “physical law” and could not be abandoned just to
save some phenomena.42 As the concept of natural law became more restricted in scope and
precise in its formulation, it also emancipated itself from the old theological underpinning.
This process of specialization and liberalization, it almost goes without saying, also affected
the concept of natural order. I will come back again on this point more extensively in the
following sections, but here I need to stress the crucial conceptual change happening in the
case of physical astronomy. Traditionally, the strikingly regularity and strictly periodicity of
the planetary motions were looked upon as the most shining example of the order of nature.
As a consequence, for classical thinkers and medieval theologians alike the periodicity of the
heavenly bodies was a metaphysical principle, an attribute of their substantial forms. Newton
disposed of the Aristotelian language of substantial forms and accepted periodicity as an
empirical fact, but his perturbation theory still made a very limited use of this fact. For New-
41
See, for example, Friedrich Steinle, “The Amalgamation of a Concept: Laws of Nature in the New Sciences,”
in Laws of Nature: Essays on the Philosophical, Scientific, and Historical Dimensions, ed. Friedel Weinert
(Berlin: De Gruyter, 1995), 316-368 and “From Principles to Regularities: Tracing ‘Laws of Nature” in Early
Modern France and England,” in Natural Law and Laws of Nature in Early Modern Europe, ed. Lorraine Daston
and Michael Stolleis (Farnham: Ashgate, 2008), 215-231.
42
See Georges Louis Buffon, “Reflexions sur la loi de l’attraction,” MARS 1749, 493-500, especially 497-498;
this paper was published on the 1745 volume of MARS.
27
�ton, periodicity comes into play as specific geometric figures as, for example, when he inter-
preted the perturbed motion of the Moon as a rotating ellipse (see below). Both the ellipse
and the circle on which it rotates have fixed geometrical features.
By contrast, in the analytical perturbation theory, periodicity became an effective and
flexible tool to treat mechanical problems. Euler’s techniques of trigonometric series and
variation of constants relied precisely on using periodicity in the most extended version as a
means to solve differential equations. Although the planetary system was still viewed as a
collection of periodic motions, periodicity was a much more complex, variegated, and com-
prehensive concept than before. This was possible because the analytical techniques made
periodicity a malleable tool of the calculus. We shall see later on that the transformation of
periodicity into a tool and its integration with the new mathematical practices would become
a key condition for the the emergence of the stability problem.
NEW PRACTICES, NEW PROBLEMS
In addition to trigonometric series and the variation of constants, late 1740s perturbation the-
ory consisted in the usual arsenal of techniques of the theory of differential equations such
as the method of successive approximations, the method of indeterminate coefficients, and
so on. From this point of view, to call it ‘theory’ is an overstatement. In fact, it was more a
collection of scattered mathematical methods and tricks than a systematized procedure. This
did not prevent mathematicians from tackling the thorniest questions of physical astronomy.
In this section, I concentrate on two episodes of special interest for the purpose of this article:
Euler’s analysis of the Great Anomaly of Jupiter and Saturn and Alexis Clairaut’s theory of
28
�the Moon. These two pieces of work show both the potentialities and the limits of pre-La-
grangean perturbation theory.
The Great Anomaly was one of the two major secular anomalies of the sky, the other
being the secular acceleration of the Moon, which will be treated in the next section. The
qualification ‘secular’ came from observational astronomy and meant a variation in the orbit
of the celestial body, generally of its mean motion, which does not cancel out after a revolu-
tion, but increases unboundedly over the centuries. In other words, secular was the exact
opposite of periodic. In the case of Jupiter and Saturn, it had long been observed that Jupiter’s
mean motion was accelerating, while, on the contrary, Saturn was slowing down. Because of
the size of the planets involved and their baffling opposite behaviors, this phenomenon was
later called the Great Anomaly or the Great Inequality. Saturn’s deceleration was particularly
perplexing because the hypothesis of the resisting ether, as we have seen above, could only
explain an increase of the mean motion. The anomaly was known to Kepler and is mentioned
extensively in a letter of Jeremiah Horrocks to William Crabtree on 26 September 1638,43
but reliable data became available only in mid-18th century. On 27 April 1746, Jacques Cas-
sini read a paper before the Paris Academy in which he explained that the comparison be-
tween ancient data and the most recent observations of Jupiter and Saturn at conjunction led
to the conclusion that the former was accelerating by 50′′ per century, while the latter was
43
Jeremy Horrocks, Opera Posthuma (London: Godbid, 1673), 320. On the history of the observations of the
Great Anomaly see Wilson, “The Great Inequality” (ref. 38), 36-39.
29
�decelerating by 2′.44 On the next meeting, three days later, Pierre-Charles Le Monnier arrived
at the same conclusion,45 but, in this case, the paper was read before the commission respon-
sible for the biannual mathematical prize sponsored by the Academy. The commission was
so impressed by the intricacies of the question that decided to make the Great Anomaly the
subject of the 1748 prize.
Euler participated in the competition and, as it was often the case, he won. Interestingly,
he begins the essay with raising several doubts on the general validity of the Newtonian law
and suggesting that it is “very probable that the action itself of Jupiter on Saturn differs con-
siderably from the inverse-square reason of the distance.”46 However, for argument’s sake,
he sets aside his doubts and tackles the problem in a Newtonian fashion. The first step is to
write down the equations of motion for radius vector, longitude, inclination, and longitude
of the ascending node.47 The equations for the two latter elements are introduced without
44
Jacques Cassini, “Des deux conjonctions de mars avec Saturne, qui sont arrivees en 1745, avec quelques
conjectures sur la cause des inegalites que l’on a remarquees dans les mouvemens de Saturne et de Jupiter,”
MARS (1746): 465-482.
45
Pierre-Charles Le Monnier, “Sur le mouvement de Saturne, et sur l’inégalité de ses révolutions périodiques,
qui dépendent de ses diverses configurations à l’égard de Jupiter,” MARS (1746): 209-222; 689-710.
46
Leonhard Euler, “Recherches sur la question des inégalités di mouvement de Saturne et de Jupiter,” (1748)
EOO II, 25, 45-157, quotation on 49.
47
In this paper Euler uses a complicated frame of reference in which all motions are referred to Saturn, whose
perturbation he wants to calculate. This explains his choice of coordinates.
30
�justification, but are identical to those obtained in 1747 by the method of variation of con-
stants. However, in the first part of the paper he only focuses on radius vector and longitude.
Euler’s general approach to perturbation problems consists in trying to solve approximately
the equations of motion for the coordinates of the body and then to derive information on the
orbital elements by means of suitable geometrical relations between the former and the latter.
This approach, as we shall see, would remain dominant in physical astronomy until La-
grange’s direct derivation of differential equations for the orbital elements in mid-1770s.
In this paper, Euler writes equations for the perturbing effects of individual elements and
then solve them by means of successive approximations. The most interesting case concerns
the effect of the eccentricity of Jupiter on the orbit of Saturn. Euler arrives at two differential
equations for the variation of the radius vector with regard to the eccentric anomaly. After
comparing equal terms, he finds the following puzzling coefficient:48
XR&0 Y ZZ [&\ Z R]W
(7) 𝑄WW =
04 R04
where B′′, P′, Q′ are other coefficients and complicated functions of trigonometric terms and
m is the ratio between Saturn’s mean anomaly and Jupiter’s. The expression (7) is obviously
a mathematical absurdity on account of the vanishing denominator 𝑚& − 𝑚& , but how should
it be interpreted? Euler claims that it entails that “a new term enters in the evaluation of the
[perturbation of the radius vector], which contains an absolute angle.”49 That is, expression
48
Euler, “Recherches” (ref. 46), 96.
49
Ibid., 97.
31
�(7) can be eliminated from the equation if one adds a term of the type 𝑇𝑝 sin 𝜔 − 𝑝 , where
ω is the elongation of Saturn, T a coefficient, and p the eccentric anomaly, i.e., the “absolute
angle.” However, this latter quantity is time-dependent, hence the additional term unbound-
edly increases with time. This is what mathematicians in the 18th century used to call an ‘arc
of circle’ and we currently dub a ‘secular term’: an expression in which a trigonometric func-
tion is multiplied by time or a time-dependent factor. The physical interpretation of such a
term was very clear to Euler:
Thus if this term enters in the expression of [the perturbation of the radius vector], the resulting
inequality, increases each revolution, as after any of these revolutions, the value of p is aug-
mented by 360 degrees: and however small the value of [T], it must, in time, happen absolutely,
that the value of this inequality surpasses any given quantity: and as it is sometimes added to
the distance of Saturn to the Sun, and sometimes subtracted, it can happen that in the same
period, Saturn approaches the Sun, and then moves away to a distance incomparably greater
than that which it draws away at present.50
Contrary to what a modern mathematician would do, Euler does not ascribe this arc of
circle to the intrinsic instability of the Jupiter-Saturn system, but rather to his gross approxi-
mation. In particular, Euler points out that the assumption of the immobility of the aphelion
of Jupiter, which he has introduced as part of the approximation, is physically wrong because
Saturn’s perturbation obviously must produce a precession of Jupiter’s aphelion. Thus, ac-
50
Ibid.
32
�cording to Euler, the arc of circle could be eliminated by means of a more accurate approxi-
mation, but he chooses to keep it in the calculation and to evaluate the coefficient T by de-
vising a very clever statistical method to combine several observational data, a technique
later brought to perfection by Laplace.51
From a mathematical point of view, arcs of circle are an annoying problem because they
entail the divergence of the trigonometric series used to approximate the solutions of the
equations of motion. More importantly, their appearance was not limited to the mysterious
Great Anomaly: they also featured prominently in the greatest success of physical astronomy
in the 1740s, Clairaut’s theory of the Moon. Among his many triumphs, Newton also faced
a burning failure in the explanation of the precession of the Lunar apogee.52 This was a phe-
nomenon well known from antiquity: the apogee of the Moon advances by about 3°3′ per
51
One can only speculate on the reasons of this apparently illogical move. Most probably, Euler considered this
analysis as an exploration of the possible causes of the Great Anomaly, rather than a fully rigorous account and
suspected that the coefficient T was responsible for the discrepancy between observations and planetary tables.
52
A useful overview of this problem and the entire Lunar theory is still Alfred Gautier, Essai historique sur le
probléme des trois corps (Paris: Courcier, 1817). More recent historical treatments of this extremely intricate
issue are Philip P. Chandler, “Newton and Clairaut on the Motion of the Lunar Apse” (PhD dissertation, Uni-
versity of California, 1975); Craig B. Waff, “Universal Gravitation and the Motion of the Moon’s Apogee: The
Establishment and Reception of Newton’s Inverse-square Law, 1687-1749” (PhD dissertation, John Hopkins
University, 1976); Craig B. Waff, “Isaac Newton, the Motion of the Lunar Apogee, and the Establishment of
the Inverse Square Law,” Vistas in Astronomy 20 (1976): 99-104; Craig B. Waff, “Newton and the Motion of
the Moon: An Essay Review,” Centaurus 21 (1977): 64-75; Curtis A. Wilson, “The Newtonian Achievements
in Astronomy,” GHA, 262-267; Curtis A. Wilson, “Newton on the Moon’s Variation and Apsidal Motion: The
33
�revolution. In other words, the lunar orbit performs a full rotation in slightly less than 9 years.
Newton analyzes the phenomenon in different sections of the Principia. Following Horrocks,
he assumes that the Moon moves along an elliptic orbit, which in turns rotates around one of
the foci.53 The perturbation analysis of this model, carried out mainly by geometrical tech-
niques, is developed partly in Book I, Section XI, Proposition 46 and partly much later in
Book III, Propositions 25-26. The practical consequences for the precession of the apogee,
however, are drawn as early as Book I and more precisely in the example 3 of Proposition
45. Using the results of the geometrical analysis, Newton finds an apogee precession equal
to 1°31′28′′, concluding dismally that “the apse of the moon is about twice as swift.”54
The failure of the great Newton and the fact that nobody was able to find a flaw in his
argument led many, included Euler as we have seen, to raise doubts about the adequacy of
the force law. Others, like Alexis-Claude Clairaut, initiated a philological revision of the
Principia to see whether the new analytical techniques could illuminate the point in which
Newton’s thought had gone awry.55 After careful investigations, Clairaut concluded that
Newton’s perturbation approach was flawed because he had neglected the transverse com-
ponent of the Sun’s perturbing force and failed to appreciate that it can also be decomposed
Need for a Newer ‘New Analysis’,” in Isaac Newton’s Natural Philosophy, ed. Jed Z. Buchwald and I. Bernard
Cohen (Cambridge, MA: MIT Press, 2001), 139-188.
53
See Book I, Proposition 44, Theorem XIV, Newton, Principia (ref. 14), 136-138.
54
Newton, Principia, (ref. 14), 147. On the details of Newton’s argument see Philip P. Chandler, “The Prin-
cipia’s Theory of the Motion of the Lunar Apse,” Historia Mathematica 4 (1977): 405-410.
55
See Alexis-Claude Clairaut, “De l’orbite de la lune dans le system de M. Newton,” MARS (1743), 17-32.
34
�into a radial and transverse component. However, this insight was hardly helpful and analyt-
ical reformulations of the apogee problem did not seem to fare any better than the old geo-
metrical ones.
In late 1746, Clairaut set out to construct a general analytical approach to the three-body
problem, a labor that occupied him throughout the 1747. In early September, he informed
Euler about his disappointing results, which he reported in an eventful meeting of the Paris
Academy on 15 November 1747.56 Clairaut considers coplanar orbits and, starting from equa-
tions of motions very similar to Euler’s, obtains a general equation for the Lunar motion:
a
(8) = 1 − 𝑔 sin 𝑣 − 𝑐 cos 𝑣 + sin 𝑣 Ω𝑑𝑣 cos 𝑣 − cos 𝑣 Ω𝑑𝑣 sin 𝑣
3
where r is the radius vector, p is a parameter depending on integration constants and the
masses of the bodies, g, c are constants, v is the true anomaly—which Clairaut prefers to
Euler’s favorite eccentric anomaly—and Ω is a complicated function of the perturbing
forces.57 The main difficulty of this equation is that Ω depends on another complicated ex-
pression ρ of the elongation and the two functions are not separable. Clairaut’s method to
56
See Alexis-Claude Clairaut, “Du systeme du monde dans les principes de la gravitation universelle”, MARS
(1747), 329-364; Clairaut’s paper was published in the MARS volume for the year 1745.
57
See Gautier, Essai historique (ref. 52); Craig B. Waff, “Clairaut and the Motion of the Lunar Apse: The
Inverse-Square Law Undergoes a Test,” GHA, 35-46; Curtis A. Wilson, “The Problem of Perturbation Analyt-
ically Treated: Euler, Clairaut, d’Alembert,” GHA, 89-107.
35
�tackle the problem is a clever combination of Euler and Newton. Like the former, he assumes
that perturbations result in an additional linear term, i.e., the solution should have the form:
a
(9) = 1 − 𝑒 cos 𝑚𝑣 + 𝜉
3
Like the latter, though, he supposes that the lunar orbit is a rotating ellipse with precession
parameter m.58 By replacing (9) in the expressions for Ω and ρ and after a considerable
amount of mathematical labor, he finally calculates the formula (1 – m) = 0,0041, which
yields a precession of the lunar apogee equal to (1 – m) × 360° = 1°30′38′′, in astonishing
agreement with Newton’s value. Facing defeat, Clairaut turns the question on its head and
investigates what force law would produce the observed precession, a move attempted by
Newton himself in the Principia (Book I, Proposition 44). His conclusion is that the gravita-
tional law must be supplemented by an additional term inversely proportional to the cube of
the distance.59
The proposal was not welcomed. Beside warding off accusations of plagiarism—Clair-
aut’s methods and arguments were suspiciously similar to Euler’s 1748 paper—he had to
counter the vehement reaction of Georges Louis Leclerc de Buffon. He was particularly vocal
in complaining that, by getting rid of the dirty water of the lunar apogee, Clairaut had also
58
Clairaut, “Du systeme du monde” (ref. 56), 345-346; A static ellipse is given by the expression 𝑝 𝑟 = 1 −
𝑒 cos 𝜈, thus m < 1 means a precession, while m > 1 means a retrogression.
59
Clairaut, “Du systeme du monde” (ref. 56), 362.
36
�thrown away the baby, i.e., the Newtonian law, a fundamental pillar of natural order.60 Clair-
aut navigated fiercely through these disputes and he was already arranging his calculations
for a comprehensive publication when, probably in late 1748, he discovered the solution of
the riddle. To ensure his priority, on 21 January 1749 he deposited at the Paris Academy a
sealed paper, which he would read much later, on 15 March 1752,61 and, on 17 March he
announced: “I have found a better method that previously indicated to reconcile the observa-
tions with the calculus.”62 The “better method” essentially consisted in a way to push the
approximation to the solution of (8) up to an higher order. In reality, Clairaut was looking
for insights on the new gravitational law, but he realized that, at the higher order, terms that
he had previously discarded became suddenly relevant. So relevant, in fact, that the resulting
expression for the apogee precession was almost exactly doubled.
Clairaut’s taming of the recalcitrant lunar apogee struck the mathematical world as a huge
success. Euler was literally thrilled about it:
The more I consider this excellent discovery, the more important it seems to me, and in my
opinion this is the greatest discovery in the theory of astronomy, without which it would be
60
Buffon, “Reflexions” (ref. 42). On the reactions to Clairaut’s theory see Philip P. Chandler, “Clairaut’s Cri-
tique of Newtonian Attraction: Some Insights into his Philosophy of Science,” Annals of Science 32 (1975),
369-375, Waff, “Universal Gravitation” (ref. 52), and Waff, “Clairaut and Apse” (ref. 57).
61
Alexis-Claude Clairaut, “De l’orbite de la lune en ne négligeant pas les quarrés des quantités de meme ordre
que les forces perturbatrices,” MARS (1749), 421-440.
62
Alexis Claude Clairaut, “Avertissement de M. Clairaut, au sujet des Mémoires qu’il a donnez en 1747 et
1748, sur le système du Monde, dans les principes de l’Attraction,” MARS (1749), 577-578, quotation on 577.
37
� absolutely impossible to succeed in determining the derangements the planets cause upon one
another in their movement. Because it is very certain that from this discovery one can regard
the law of attraction [by the] inverse ratio of the square of the distance as solidly established,
on which depends all the theory of astronomy.63
For many scholars, especially for mathematicians of the new generation, Clairaut’s tri-
umph closed the search for the causes of celestial phenomena: the explanation of planetary
motions had to be provided exclusively in terms of gravitational interactions. Others were
not so easily convinced. Euler, despite his initial enthusiasm, maintained his belief of an
interplanetary ether and the incompleteness of the gravitational law for many years.64 In ad-
dition, Clairaut’s theory also encountered arcs of circle. They first crop up in 1747 in the first
order solution to (8). On that occasion, Clairaut gets rid of them by choosing some undeter-
mined coefficients such that the time-dependent factor becomes zero, which essentially
amounts to specifying in advance the form of the solution.65 But then they appear again in
the ameliorated theory and there Clairaut follows Euler in attributing the problem to his as-
sumption that the apogee of the Sun is at rest. However, the fact that the arcs of circle could
be found even in the equations of a periodic phenomenon such as the precession of the lunar
63
Leonhard Euler to Alexis-Claude Clairaut, 29 June, 1751 in Gabriel Bigourdan, “Lettres inédites d’Euler à
Clairaut,” Comptes Rendu de du Congrès des Sociétés savants, Section de sciences, Lille 1928 (Paris, 1930) 26-
40, quotation on 36-37.
64
See, for example, Leonhard Euler to Tobias Mayer, 25 December 1751 in Eric G. Forbes, The Euler-Mayer
Correspondence (1751-1755) (New York: American Elsevier, 1972), 45.
65
Clairaut, “Du systeme du monde” (ref. 56), 349-350.
38
�apogee, seemed to suggest that they were not related to physical conditions, but rather to the
mathematical techniques used in perturbation theory. This suspicion was confirmed in 1766
by an ingenious argument of the young Joseph Louis Lagrange.
More a mathematician than an astronomer, Lagrange saw the issue of the arcs of circle
from a formal point of view and dealt with it as part of the theory of integration of differential
equations.66 He notices that all problems in perturbation theory can be reduced to integrating
the following equation:
L4f
(10) + 𝐾 & 𝑦 + 𝐿 + 𝑖𝑀𝑦 & + 𝑖 & 𝑁𝑦 n + ⋯ = 0
Lg 4
where K, L, M, N, are coefficients. The first three terms refer to the unperturbed case, while
the rest of the equation gives the different orders of approximation for the parameter i, which,
in physical astronomy, is generally the mass of the perturbing planet. The standard solution
technique, used by Euler and Clairaut, consists in finding the integral for the unperturbed
case, replacing it into y2 while disregarding the higher terms, finding the new integral, replac-
ing it into y3 and so on for all desired orders. This apparently reasonable procedure, called
successive approximations, has a fatal flaw. Lagrange realizes that the successive integrals
of (10) are in fact special cases of the general integral of the equation:
66
Lagrange discusses the problem on the arcs of circle in Joseph Louis Lagrange, “Recherches sur les inégalités
des satellites de Jupiter causées par leur attraction mutuelle,” (1766) OLG, VI, 67-225 and more extensively in
“Solution de différents problèmes de calcul intégral,” (1766) OLG, I, 609-668. The former paper was published
much later in 1777.
39
� L4f
(11) + 𝐾 & 𝑦 + 𝐿 + 𝑎 cos 𝛼𝑡 + 𝑏 cos 𝛽𝑡 + ⋯ = 0
Lg 4
Clairaut encounters a similar equation, although not is such a general form. The integral of
(11) is the following:
v x *
(12) 𝑦 = 𝑓 cos 𝐾𝑡 + sin 𝐾𝑡 + cos 𝐾𝑡 − 1 + cos 𝐾𝑡 − cos 𝛼𝑡
w w4 w 4 Ry 4
𝑏
+ cos 𝐾𝑡 − cos 𝛽𝑡 + ⋯ = 0
𝐾& − 𝛽&
The gist of Lagrange’s argument is now that the results of successive approximations on (10)
are integrals of the form (12) in which K = α, which is precisely the case found by Euler in
1748. To understand what happens in this case, Lagrange assumes that K = α + ω and then,
taking the limit as ω goes to zero, he shows that the following term appear:
*
− 𝑡 sin 𝐾𝑡
&w
which is an arc of circle.67 This means that, already at the first order, and consequently at any
higher order, the method of successive approximations applied to the equations of physical
astronomy produces necessarily arcs of circle. He correctly individuates the problem in the
iterative procedure of the method and construes a new way of integrating the equations that
avoids the iteration and it is therefore free of the arcs of circle.68
67
Lagrange, “Solution” (ref. 66), 554-555 and Lagrange, “Satellites de Jupiter” (ref. 66), 110-112.
68
Lagrange, “Solution” (ref. 66), 562-566.
40
� But Lagrange’s clever maneuver could not eliminate the uneasiness of the younger gen-
eration of mathematicians toward the current state of physical astronomy. Perturbation theory
had several structural problems. The methods of Euler and Clairaut had scored remarkable
successes, but, as the issue of the arcs of circle demonstrated, they were instruments that
could perform at best only in the hands of real virtuosi. Perturbation theory lacked a system-
atic and procedural structure that could enable the practitioners—any practitioner, in fact—
to distinguish between formal artifacts and genuine information. In addition, the calculations
were exceedingly complex—even Euler made several computational mistakes in his 1748
paper, which led him to the absurd conclusion that both Jupiter and Saturn were in fact ac-
celerating. More importantly, it was dauntingly difficult to extend the perturbations beyond
a certain order of approximation and, as Clairaut’s theory showed, many crucial results were
hidden at higher orders. It was therefore essential to develop new mathematical practices to
select the terms on which to perform the perturbation analysis and to extract information
from the equations of motion even before starting to explicitly solve them.
PERTURBATION THEORY COMES OF AGE
During the 1770s, two developments led progressively to the problem of stability. On the one
hand mathematicians grew increasingly skeptical about the reality of secular inequalities. On
the other, there was a sustained effort, especially by Lagrange, to make perturbation theory
more reliable, robust, controllable, and systematic. This body of work was mainly carried out
through the analysis of concrete physical problems and these problems became conceptual
41
�laboratories in which new mathematical techniques could be tested and improved. In this
section I discuss these two developments in detail.
DOUBTS ON SECULARITY
Three results, two theoretical and one observational, seriously undermined the belief in
the reality of secular, to wit strictly non-periodic, inequalities. The first result is Laplace’s
famous proof of the invariability of the mean motions, the work often indicated as the first
proof of stability of the solar system.69 In the first part of this long paper, Laplace examines
thoroughly the gravitational law and singles out four fundamental assumptions. The first one
is the mathematical essence of the law: the attraction is directly proportional to the masses of
the bodies involved and inversely proportional to the square of their distance. In support of
this posit, Laplace offers an ingenious dimensional argument according to which, if one
grants the (almost metaphysical) hypothesis that the global behavior of the universe is scale-
invariant, then it follows that the inverse-square law is the most obvious choice.70 The second
69
Pierre Simon Laplace, “Sur le principe de la gravitation universelle er sur les inegalités séculaires des planétes
qui en dépendent,” (1771) OLP, VIII, 201-275. The bibliographical history of this paper is rather complicated
and makes it difficult to untangle possible influences and connections. It was a two-part piece, the first of which,
dedicated to integration theory and theory of probability, was read at the Paris Academy on 10 February 1773.
The second part, on gravitation, was probably read much earlier, on 27 November 1771, but was published only
in 1776. On the intricacies of Laplace’s bibliography, see Stephen M. Stiegler, “Laplace’s Early Work: Chro-
nology and Citations,” Isis 69, no. 2 (1978): 234-254 and Charles G. Gillispie, Pierre-Simon Laplace 1749-
1827. A Life in Exact Science (Princeton, NJ: Princeton University Press, 1997).
70
Laplace, “Le principe de la gravitation,” (ref. 69), 214-215; see also Morando, “Laplace”, (ref. 3), 132-133.
42
�assumption is that the attractive force is equally exerted (and equally felt) by each particle of
a body. Having in mind a work of Lagrange that we shall examine shortly—and that he quotes
in another section of the paper—Laplace states that this assumption is supported by the irrel-
evance of the figure of the Earth for the motion of the Moon. The third assumption, i.e., the
instantaneous propagation of gravity, is accepted for lack of contrary evidence. In fact, La-
place calculated that a finite velocity of propagation could account for the secular accelera-
tion of the Moon provided that this velocity be equal to about six million times the speed of
light. The fourth and final assumption, that the gravitational attraction does not depend on
the state of motion of the body, deserves a more careful discussion. From a kinematic point
of view, the negation of this assumption is equivalent to the hypothesis of a resisting medium:
if the space is pervaded by a medium, its action will change with the state of motion of the
body. In fact, Laplace proves that also this hypothesis would provide a handy explanation of
the secular acceleration of the Moon.71 However, Laplace is “far from considering as certain
[…] that the secular equation of the Moon exists”72 and he also strongly doubts the existence
of a resisting medium. Unlike the mathematicians of the previous generation, for Laplace
there is no question that an explanation of the secular inequalities, if they exist at all, must
be found within the gravitational theory alone. The issue, rather, is whether the planetary
interactions suffice.
71
Ibid., 221-227.
72
Ibid., 234.
43
� It is important to stress that Laplace’s skepticism about the existence of secular inequali-
ties does not entail an interest in the stability of the solar system. A discussion of the details
of Laplace’s analysis of the secular inequalities will reinforce this point. Like Euler, Laplace
begins with writing the equations of motion for radius vector and longitude and proceeds to
solve them for these coordinates. His first departure from the traditional procedure consists
in writing the solution of the unperturbed problem as an infinite trigonometric series. The
reason for this move becomes immediately clear. If one replaces this solution in the perturbed
equations, an identity between the two sides follows. Laplace points out that, in order to study
secular inequalities, “it suffices to take into account, [in the perturbed equation for the radius
vector], only the constant terms and those that increase with time; in the [equation for the
longitude] it is necessary to consider also the coefficients of cos 𝑛𝑡 + 𝜀 and sin 𝑛𝑡 + 𝜀 .”73
This approach is Laplacian through and through: he does not waste time in pondering the
general problem, but he straightforwardly concentrates on the terms that are likely to con-
tribute to the secular inequalities. His goal is to calculate the coefficients of these terms in
order to establish whether they are secular or periodic.
By this method Laplace obtains general formulas for inequalities due to perturbations and
then goes on to apply these arguments to the Great Anomaly. But when Laplace plugs obser-
vational data in his formulas, he finds a baffling outcome: “by substituting those values in
the formula for the secular equation, I have found them absolutely null: from this I conclude
that the alteration of the mean motion of Jupiter, if it exists, is by no means due to the action
73
Ibid., 243; Laplace is referring to the coefficients related to the mean motions.
44
�of Saturn.”74 Laplace quickly realizes that this result is not a peculiarity of the Great Anom-
aly.75 By using recursive formulas calculated by D’Alembert and Lagrange for the coeffi-
cients of the terms of interest, he manages to prove that those coefficients cancel each other
out and leave the semi-major axes (or the mean motions) identically zero. Although this result
has often been regarded as the first proof of the stability, Laplace does not draw any such
consequence from his arguments. From his point of view, he has simply answered in the
negative the question whether the planetary interaction can produce secular inequalities. This
null result only entails that the reason for the inequalities must be sought outside the planets:
It follows from the preceding theory that these variations cannot be attributed to the mutual
action of these two planets. But if one considers the large number of comets that move around
the sun; if one reflects further that very possibly some of them have passed close enough to
Jupiter and Saturn to alter their movements, and that their effect, other things being equal, must
be greater on the planets farther from the sun, for the same reason that the effect of Jupiter and
Saturn is greater than its effect on Mars, though it is closer to Mars than to Saturn, one will
regard it as very probable that the variations observed in the mean movements of Jupiter and
Saturn have been produced by the action of these comets.76
Hence, far from considering the stability of the solar system as a problem, Laplace is in
fact assuming it. Although not directly related to the stability of the solar system, Laplace’s
74
Ibid., 253.
75
In fact, Laplace also puts forward a more general argument, based on the conservation of angular momentum,
to prove that Saturn’s gravitational action cannot produce Jupiter’s acceleration.
76
Ibid., 253-254.
45
�proof of invariability of the mean motions, and particularly its application to the Great Anom-
aly, raised reasonable doubts on the reality of secular inequalities. Another finding that rein-
forced these doubts became known about the same time as Laplace’s paper. In the early
1770s, the Prussian Academy of Science launched a project to publish in a unified fashion
the most important astronomical tables of the time, including Mayer’s celebrated tables of
the Moon, Halley’s ones of the planets and Wargentin’s computations of the satellites of
Jupiter. The project, eventually completed in 1776, was not a mere collection: it involved a
recalculation of the old tables and their recalibration on the Berlin meridian. Johann Heinrich
Lambert was one of the mathematicians collaborating to this endeavor. In 1773, Lambert
used advanced perturbation techniques77 to produce new tables of Jupiter and Saturn.78 The
result was surprising. From the mid-17th century the Great Anomaly appeared to go back-
wards: Saturn was accelerating and Jupiter was slowing down! Of course, such behavior was
not compatible with a genuinely secular inequality.
On his part, Lagrange had probably begun to think that the inequalities in the solar system
were in fact periodic around the time of his move to the Prussian Academy, at the end of the
1760s or in the early 1770s. He makes unequivocally this point in very same paper used by
Lambert to compile his tables: “it would appear very probable that [secular] inequality are
77
Most probably Lambert took his methods from Joseph Louis Lagrange, “Recherches sur la manière de former
des tables des planètes d’après les seules observations” (1772) OLG, VI, 507-627.
78
See Johann Heinrich Lambert, “Résultat des recherches sur les irrégularités du mouvement de Saturne et de
Jupiter,” Nouveaux Mémoires de l’Academie Royale de Berlin (1773), 216-221.
46
�only apparent and only come from some equations of which the arguments vary but little, so
that their period is very long.”79
But what definitely confirmed this belief was his study of the secular acceleration of the
Moon. Among the celestial anomalies, the secular acceleration of the Moon has the most
peculiar story.80 It was announced for the first time by Edmond Halley in a paper read at the
Royal Society on 19 October 1692. However, Halley later doubted his conclusion and New-
ton, who mentioned the phenomenon in the second edition of the Principia (Book III, Prop-
osition 42), had the reference removed in the third edition. For nearly fifty years the phenom-
enon not only figuratively, but literally disappeared from the astronomical map until Richard
Dunthorne rediscovered it in 1749. Dunthorne took up the endeavor of preparing new Lunar
tables based on Newton’s theory and systematically examined the six major eclipses of the
past. The key eclipse of Dunthorne’s analysis had been observed on 22 December 383 B.C.
in Babylon. The peculiarity of this eclipses lay in the fact that, according to Dunthorne’s new
tables, Babylonians should have not seen it at all because the Moon should have already set!
The bare fact that an eclipses was recorded proved that the mean motion of the Moon was
79
Lagrange, “Tables des planètes” (ref. 77), 511.
80
For a full account see David Kushner, “The Controversy Surrounding the Secular Acceleration of the Moon’s
Mean Motion,” Archive for History of Exact Sciences 39, no. 4 (1989): 291-316; John M. Steele, “Dunthorne,
Mayer, and Lalande on the Secular Acceleration of the Moon,” in Ptolemy in Perspective. Use and Criticism of
his Work from Antiquity to the Nineteenth Century, ed. Alexander Jones (New York: Springer, 2010), 203-229;
John M. Steele, Ancient Astronomical Observations and the Study of the Moon’s Motion (1691-1757) (New
York: Springer, 2012).
47
�faster in Dunthorne’s times than in the past. He calculated the total acceleration to be 10′′ per
century. Another great astronomer, Tobias Mayer, reached the same conclusion in 1753.
Mayer’s lunar tables, based on Euler’s perturbation theory, were unanimously praised as the
most precise available. He slightly corrected Dunthorne’s value of the acceleration to about
6′′ per century. In 1757, the secular acceleration received its ultimate sanction by Joseph-
Jerome Lalande, whose tables, compiled on the basis of Clairaut’s theory, confirmed the ac-
celeration as well as Dunthorne’s value.
Thus, when, in 1774, Lagrange participated to yet another Paris Academy prize dedicated
to the behavior of the Moon, the unbounded acceleration of its mean motion was just a boring
scientific truth. However, the first part of Lagrange’s paper is concerned with provocatively
proving that the evidence in favor of the reality of the secular acceleration is not as robust as
generally believed. He challenges the reliability of the data concerning ancient eclipses and,
above all, argues that the data are compatible with the hypothesis of a periodic phenomenon
of very large period:
[T]he problem of the secular equation of the Moon, from this point of view, is entirely unde-
termined and cannot be solved by resorting to the observations alone. […] It is therefore by
means of the theory that one can aspire to determine the form of the secular equation of the
planets and the Moon in particular.81
81
Joseph Louis Lagrange, “L’Équation séculaire de la lune” (1774) OLG, VI, 335-399, quotation on 344-345.
48
� Most of the other factors having already been investigated, the only plausible cause of the
(alleged) secular equation was the non-sphericity of the Earth. Hence, Lagrange proceeds to
improve the theory in order to verify whether the assumption of a non-spherical Earth can
change the orbit so dramatically to produce the observed acceleration. His perturbation
method is still Eulerian: he writes the equations of motion for the coordinates and then adds
the radial and tangential perturbations due to the Sun. The trickiest part of the analysis is how
to codify the non-sphericity into the equations of the perturbed motion. Lagrange’s solution
is, as usual, very ingenious and is based on a way “to consider in particular the attraction of
each particle of the Earth on the Moon and to find the resultant force.”82 In brief, he imagines
the Earth decomposed into infinitesimally small elements, considers the attraction exerted by
each element on the Moon and them sum them up to find the resultant. In his calculation he
assumes that the Earth is a symmetric and uniformly dense body—he would relax these as-
sumptions later—and expresses the Earth-Moon distance in trigonometric series of the dec-
lination of the Moon.
The next problem is to define a criterion of secularity in terms of the coordinates used to
write the equations of motion. Lagrange focuses on the ratio between the radial force (the
most active force in the lunar motion) and the square of the radius vector. He manages to
prove that if one can find a constant term (or equivalently, the sinus of a very small angle) in
this ratio, then the equation of the mean motion is increased by a quantity depending on the
square of the time, i.e., there is a real secular acceleration. By contrast, if the ratio contains a
82
Ibid., 348.
49
�certain periodic term, then the mean motion is increased by a periodic trigonometric factor
and the secular acceleration is, as a matter of fact, periodic. Armed with a criterion to decide
the question, Lagrange integrates the equations of motion, which contain the effect of the
non-sphericity of the Earth, and concentrates on the important ratio, which he assumes to be
a trigonometric series of five angles. By a compelling argument, he shows that the five angles
can be reduced to a single angle depending on the true anomaly of the Sun, the Sun-Moon
distance, and the longitude of the Moon and, finally, that the ratio can only generate a periodic
term. Hence, the non-sphericity of the Earth has nothing to do with the secular acceleration.
ENLARGING THE WEAPONRY
Lagrange’s negative conclusion about the secular acceleration of the Moon stirred the
fierce opposition of the astronomers. Led by Le Monnier, they protested that observations
unequivocally indicated an increase of the mean motion. But the skepticism was already
spread among mathematicians. In a letter, Jean D’Alembert agreed on the “uncertainty” of
the phenomenon,83 and Lagrange responded that, although astronomers were “very attached
to the secular equation,” the arguments against it were “incontestable.”84 Once settled this
point, in the remainder of the decade Lagrange dedicated himself mainly to make perturba-
tion analysis a more robust, reliable, and standardized theory. From 1774 to 1777, he changed
83
Jean D’Alembert to Joseph Louis Lagrange, 25 April 1774, in Joseph Louis Lagrange, “Correspondance et
Mémoires Inédits” (1882) OLG, XIII-XIV, quotation on XIII, 282.
84
Joseph Louis Lagrange to Jean D’Alembert, 21 May 1774, Ibid., XIII, 284.
50
�dramatically the way of treating perturbations by introducing a series of innovative mathe-
matical methods.
In this regard, the first place to look at is his study of the secular variations of planetary
inclinations and nodes.85 What immediately strikes the reader of this paper is that, for the first
time, perturbation analysis is extended to an arbitrary number of planets. To overcome—
partially—the difficulties of this extension, Lagrange exploits ingeniously the concept of in-
tegrals of motion to simplify the computation procedure. After writing the usual equations of
motion, he introduces the ‘integrals of area’, related to what we would call the angular mo-
mentum:
fL}R~Lf }L~R~L} }LfRfL}
(13) 𝑃= , 𝑄 = , 𝑅 =
Lg Lg Lg
where x, y, z are the coordinates of the body. From these integrals he can derive the equation
of the orbital plane, which turns out to be 𝑃𝑥 − 𝑄𝑦 + 𝑅𝑧 = 0. The plane passes through the
origin of the coordinates and intercepts the plane xy in the line of nodes. Lagrange shows
easily that the tangent of the angle ω between this line and the axis x—i.e., the usual longitude
of the node—is equal to 𝑃/𝑄, while the tangent of the inclination between the orbital plane
85
Joseph Louis Lagrange, “Recherches sur les équations séculaires des mouvements des noeuds et des inclinai-
sons des orbites des planétes” (1774) OLG, VI, 635-709. It must be noticed that here, by secular, Lagrange does
not mean ‘unbounded’, but rather ‘long-term’, i.e., variations over a long span of time. More on this semantic
shift later.
51
�and the plane xy, which Lagrange calls θ, is equal to 𝑃& + 𝑄& 𝑅. From this, Lagrange finds
the beautiful relations:
\ ]
𝜃 sin 𝜔 = , 𝜃 cos 𝜔 =
ƒ ƒ
which show that inclination and line of node are conjugate variables. This remarkable sym-
metry is at the origin of one of Lagrange’s most valuable contributions, the so-called La-
grangean coordinates:
(14) 𝑠 = 𝜃 sin 𝜔 , 𝑢 = 𝜃 cos 𝜔
These coordinates are a powerful tool to study the variation of the orbital elements. From a
computational point of view, they entail an immediate simplification of the problem, because
the equations of motion for the new coordinates assume the elegant form:
L… Lƒ Lˆ Lƒ
(15) 𝑅 + 𝑠 = 𝑌𝑧 − 𝑍𝑦, 𝑅 + 𝑢 = 𝑋𝑧 − 𝑍𝑥
Lg Lg Lg Lg
where X, Y, Z are the components of the perturbing force. Exploiting the symmetries of the
problem, the transformation of coordinates reduces the usual second-order differential equa-
tions of motion to the first-order system (15). Even more importantly, equations (15) contain
the crucial Lagrangean idea of shifting the focus of the analysis from the coordinates of the
body to the time variation of the orbital elements. From a conceptual point of view, this
departure from Euler’s classical approach means to replace the study of the trajectory of the
52
�body in terms of coordinates with the study of the changing geometry of the orbit in terms of
orbital elements.86
Another crucial innovation happens when Lagrange introduces explicit expressions for
the perturbing forces X, Y, Z in the equations (15). The gravitational forces always encumber
the notation because they contain the ratio between the masses of the bodies and their dis-
tances, generating an intricate forest of symbols, which makes calculations lengthy, difficult,
and prone to mistakes. Lagrange introduces a new notation for the typical force term:
Š‹ 3‹ 3Œ, ,3‹
(16) = 𝑖, 𝑗
•Ž3Œ
where Mj is the mass of the j-th planet, rj its distance from the Sun, (ri, rj) the distance between
the i-th and the j-th planet and μ is the proportionality factor of the mean motions. This new
parenthetical notation polishes the mathematician’s sheet, facilitates the computation, keeps
mistakes under control, and highlights the internal symmetries in the system of equations.87
86
This idea had been partly anticipated by Charles Euler, Leonhard’s third son, in his prize award essay “Med-
itationes in quaestionem utrum motus medius planetarum semper maneaet aeque velox, an successu temporis
quampiam mutationem patiatur? Et quoenam sit ejus causa?,” Recueil des pieces qui ont remporte les prix de
I’Academie royale des sciences, VIII (1760), 1-45.
87
In fact, this is one of the first instances of a tendency that would established itself in the 19th century mathe-
matical physics, to wit the introduction of compact notations to ease the calculation. The Poisson brackets and
Einstein’s index summation convention are other notable examples.
53
� The power of these new techniques becomes visible when Lagrange integrates the equa-
tions (15) to calculate the secular variation of inclinations and nodes. He shows that, when
forces are plugged in, the equations turn out to be separable into a linear and a periodic part,
the latter being composed of trigonometric functions only. One can discard this part: “since
one wants to abstract from those kinds of inequalities and to investigate only the motions of
the nodes and the variations of the inclinations insofar as they are independent of the motion
of the planets themselves along their orbits, one can immediately reject those [periodic
terms], which makes the differential equations [for the new coordinates] very simple and
easy to integrate.”88 If one confines oneself to the case of two planets, the equations of motion
in the new notation are simply:
L… Lˆ
(17) + 0,1 𝑢 = 0, + 0,1 𝑠 = 0
Lg Lg
whose solution is a superposition of harmonic vibrations. The general form of the solution is
given by the characteristic equation for the amplitudes of these vibrations whose degree is
equal to the number of planets.89 In particular, if the roots of this equation are all real and
unequal, the system (17) has a finite solution and it is possible to know the values of inclina-
tion and nodes at any instant provided that one knows the initial values. Lagrange mentions
in passing that if there are pairs of equal roots or if the roots are imaginary, then arcs of circle
88
Lagrange, “Noeuds et inclinaisons” (ref. 85), 647.
89
In 1766, Lagrange had deployed the same procedure to calculate the equilibrium stability of n vibrating
strings, see Lagrange, “Solution” (ref. 66), 520-534.
54
�and exponentials appear in the solution.90 Lagrange does not comment on this important
point, but it will crop up again, as we shall see.
Lagrange’s new mathematical methods brought notational, computational, and conceptual
innovations in perturbation analysis. He was wholly aware that his approach was “worthy of
the attention of geometers, independently of the use that it can have in astronomy.”91 Argua-
bly the most remarkable and enduring among Lagrange’s many improvements was his strat-
egy to construct equations for the orbital elements, rather than the body’s coordinates. To
develop fully this idea, he came back to Laplace’s great feat, i.e., the invariability of the mean
motions. In a paper presented at the Berlin Academy on 24 October 1776—but published
only in 1779—Lagrange argues that Laplace’s invariability proof, albeit impressive, is still
incomplete because he assumes quasi-circular and quasi-coplanar orbits and it is limited to
the third order of eccentricity and inclination. However, the extension of the approximation
to higher orders requires extremely lengthy and complex calculations, far beyond the possi-
bility of a human being. “Fortunately”, he continues, “I have found a means to prove [this
invariability] a priori and without supposing that the planetary orbits are nearly circular.”92
90
Lagrange, “Noeuds et inclinaisons” (ref. 85), 665.
91
Joseph Louis Lagrange to Jean D’Alembert, 6 June 1774, in Joseph Louis Lagrange, “Correspondance” (ref.
83), quotation on XIII, 287.
92
Joseph Louis Lagrange, “Sur l’altération des moyens mouvements des planétes” (1776) OLG, IV, 255-271,
quotation on 258.
55
� His argument seems to anticipate ideas that will be developed by Jacobi and Hamilton
several years later. He points out that a general solution of the equations of motion is given
by six equations of the form 𝑉 = 𝑘, where k is an orbital element and V a function of the
coordinates and their first derivatives. In the unperturbed case, the elements are constants of
motion, i.e., 𝑑𝑉 = 0, but if perturbations are turned on, the elliptic orbit is free to change,
therefore 𝑑𝑉 = 𝑑𝑘, which is a general expression of the variation of constants. This simple
consideration is the cornerstone to derive a very elegant equation for the variation of an ar-
bitrary element in terms of the function V and the perturbing forces:
L‘ L+ L+ L+
(18) =− ’“ 𝑋− ’• 𝑌− ’– 𝑍
Lg L L L
’” ’” ’”
where X, Y, Z, are, as usual, the components of the perturbing force. From this equation it is
simple to calculate the time variation of the semi-major axis. A little geometry allows La-
grange to determine the function V for the unperturbed case and an application of (18) yields
immediately:
X —L}[˜L}[™L~
(19) 𝑑 =
&* š
where a is the semi-major axis and F is the gravitational attraction of the Sun.
Now Lagrange has to face again the usual problem of expressing the whole perturbing
action in a computationally efficient way. His solution is a brilliant one: he expresses the
numerator on the right-hand side of (19) as a brand new ‘perturbing function’, so that the
equation for the semi-major axis assumes the general form:
56
� X ›œ
(20) 𝑑 =
&* •[ž
where S and T are the masses of the Sun and the planet respectively. As the perturbing func-
tion Ω is, in fact, a potential function, the partial derivative in (20) refers to the fact that the
function must be differentiated with respect to the coordinates and then summed up. From a
conceptual point of view this is a huge advancement because Lagrange is regarding pertur-
bation not as composition of forces, but in a truly analytical way as an alteration of the space
around the perturbed body.93 By integrating equation (20) for a body perturbed by an arbitrary
number of planets, Lagrange shows that the formula for the mean motion is a ratio whose
numerator is a trigonometric series, while the denominator is:
*2 *2
(21) 𝑚+𝑛 +𝑝 +⋯
*Ÿ2 *42
where m, n, p, …, are positive numbers and the ai are the semi-major axes of the perturbing
planets. Hence, the semi-major axes remain bounded if and only if (21) is never zero or,
which is the same, if the mean motions of the planets are pairwise incommensurable. But
then, according to Lagrange, the invariability is guaranteed because “it is easy to convince
oneself that [the case in which (21) is zero] cannot take place in our system, where the values
93
Lagrange would further refine the concept of perturbing function in Joseph Louis Lagrange, “Remarques
générales sur le mouvement de plusieurs corps qui s’attirent mutuellement en raison inverse des carrés des
distances” (1777) OLG, IV, 401-418. This paper was published in 1779. Most of the research in physical as-
tronomy in the 19th century would be based on finer and finer approximations of the perturbing function in
order to calculate the orbits of planets, comets, and satellites.
57
�[of the mean motions] are all incommensurable.”94 This statement is puzzling. First of all,
one cannot exclude the commensurability of the mean motions on observational grounds be-
cause observations only yield rational numbers. Furthermore, there is in fact a case of quasi-
commensurability in the solar system: the ratio between the mean motions of Jupiter and
Saturn is almost exactly 5/2, a circumstance that should immediately suggest a relation be-
tween Lagrange’s arguments and the Great Anomaly. But, at this stage, this relation goes
unnoticed. The spotlight, instead, is placed almost completely on the novel mathematical
techniques introduced by Lagrange in treating the orbital elements. After the publication of
the article, Laplace summarized Lagrange’s great achievements with almost lyric overtones:
The felicitous application of the beautiful method that you have explained at the beginning of
your memoir, involving finite partial differences; the extremely simple formula which you ob-
tain for the variation of the major axis; your shrewd observation that in integrating this formula
it is only necessary to take account of the variation of the coordinates of the perturbed planet,
and the consequence that follows thereupon, provided that the mean movements of the planets
are mutually incommensurable, that the variations of their major axes are necessarily peri-
odic—all that, along with the elegance and the simplicity of your analysis, has given me a
pleasure that I cannot put into words.95
To our eyes, Laplace’s comments might appear overly flattering, but it is undisputable
that, in the 1770s, Lagrange elevated perturbation theory from a collection of disconnected
94
Lagrange, “Moyens mouvements” (ref. 92), 270.
95
Pierre Simon Laplace to Joseph Louis Lagrange, 10 June 1779 in Lagrange, “Correspondance” (ref. 83),
quotation on XIV, 83-84.
58
�rules and procedures to a set of robust and reliable mathematical practices tightly related with
other mathematical fields such as the theory of differential equations and potential theory.
Times were ripe to harvest the fruits of this work.
THE CO-COSTRUCTION OF STABILITY
HOW THE SOLUTION DETERMINED THE PROBLEM
During the 1770s, Lagrange attacked the issue of secular inequalities from a variety of angles.
In his study of the lunar motion he argued that the secular acceleration simply did not exist.
In the same year, he proposed new sophisticated techniques to deal with the equations of
motion in order to isolate the secular contribution of nodes and inclinations. Finally, in 1776,
he developed general arguments to handle the variation of orbital elements. This work cul-
minated in a two-part paper on secular inequalities. It is in this paper that, for the first time,
the problem of the stability of the solar system is explicitly mentioned. Initially, Lagrange
lays down the traditional distinction between periodic inequalities, “which depends on the
mutual configurations of the planets,” and secular inequalities, “which appears to increase
constantly.”96 For the first time, Lagrange relates secularity with the long-term stability of
the system: “the latter [inequalities] change the very elements of the orbit […] and although
96
Joseph Louis Lagrange, “Théorie des variations séculaires des élements des planétes. Première partie con-
tenant les principes et les formules générales pour déterminer ces variations” (1781) OLG, V, 125-207, quota-
tion on 125.
59
�their effect is insensible within a short range of time, it can become sizable in the long run.”97
While here ‘secular’ still means ‘unbounded’ and ‘aperiodic’, we shall shortly see how La-
grange alters profoundly the semantics of the term.
But before getting at that, Lagrange develops his “more direct and more rigorous” treat-
ment of secular inequalities, which relies on the techniques introduced and refined during the
previous decade. He extends the argument used in 1774 to the secular variations of semi-
major axis, eccentricity, and inclination, i.e., the orbital elements whose change can modify
dramatically the form of the orbit. He introduces new coordinates for these elements analo-
gous to those deployed for inclinations and nodes and makes use of the perturbing function
to represent the forces. The result is a set of differential equations for the elements of interest.
The secular behavior of the orbit can be derived by integrating these equations, but before
doing this, Lagrange comes back to the concept of secularity. At the beginning of the second
section, he defines secular inequalities as “those without a fixed period or at least a very long
one and independent on the return of the planets to the same points of their orbits.”98 Here
the usual opposition between periodic and aperiodic inequalities is replaced by a new dualism
between short period (i.e., a single revolution) and long period (to be calculated for any in-
dividual case). In this way, secular inequalities are viewed as a more complex type of periodic
inequalities. Unbounded inequalities, Lagrange believes, do not exist. The appearance of
aperiodicity stems from the extremely long period of some inequalities. Undoubtedly, the
97
Ibid., 126.
98
Ibid., 147.
60
�multiple objections against secularity accumulated over the 1770s prepared this redefinition
of secularity, which defies openly the tradition of observational astronomy and paves the way
to the concept of stability of the solar system.99
Lagrange moves his first step toward this concept by generalizing the proof of invariability
of the mean motion, which he formulates for his new coordinates. Next, he goes on to treat
inclination and eccentricity. In 1774, Laplace had extended Lagrange’s treatment of inclina-
tion and node, showing that also eccentricity and longitude of the aphelion are conjugate
elements.100 Now Lagrange exploits this full symmetry to construct a generalization of his
1774 argument that embraces all elements. In this way, he can finally formulate general equa-
tions yielding the annual variation of mean motion, eccentricity, and inclination and he con-
cludes that “the problem of the secular inequalities is then analytically solved because it is
reduced to equations whose integration is known.”101 But this only provides half of the solu-
tion, i.e., general equations for the secular variation of the orbit. Now Lagrange has to inte-
grate these equations for the individual planets and show that no divergence appears, which
is what he does in a second part of his work, read the following year. Although the application
99
This new notion of secularity would quickly become standard among mathematicians. For one, Laplace
adopted it wholeheartedly, see Pierre Laplace, Exposition du Système du Monde (1796) OLP, VI, 1-479, on
222-223 and Traité de mécanique celeste (1799-1825) OLP, I-IV, I, 327.
100
See Pierre Simon Laplace, “Mémoire sur les solutions particuliéres des équations différentielles et sur les
inégalités séculaires des planétes,” (1774) OLP, VIII, 325-366.
101
Lagrange, “Théorie des variations séculaires I” (ref. 96), 194.
61
�of the general theory “does not have other difficulties than the lengthiness of the calcula-
tion,”102 the final results are severely undermined by the uncertainty about the planetary
masses. But Lagrange’s real goal is to examine the long-term behavior of secular inequalities
for which one needs to integrate the differential formulas, “because only this knowledge can
enable us to decide the important question of the stability of our planetary system.”103
It is at this moment, 55 years after Newton’s death, that the “important question” of sta-
bility finally rises to the dignity of a scientifically decidable question. Lagrange points out
that, as the invariability of the mean motions (“the main point of this question”) has been
already established, the system can be declared stable if the integrals of the differential equa-
tions for inclination and eccentricity do not contain arcs of circle. As yet another ironic twist
in this story, the arcs of circle, once a major flaw of physical astronomy, are now used as
stability criterion. This can happen because Lagrange’s numerous refinements of perturba-
tion theory allow him to control the arcs of circle and to distinguish reliably the cases in
which they represent a formal artifact and those in which they provide genuine physical in-
formation.
Lagrange had already shown in 1774 how to integrate the equations for inclinations and
eccentricity. Using his clever coordinates change, they can be reduced to a system of first-
order differential equations whose solutions are combinations of harmonic oscillations. The
102
Joseph Louis Lagrange, “Théorie des variations séculaires des élements des planétes. Seconde partie con-
tenant la ces variations pour chacune des planètes principales,” (1782) OLG, V, 211-344, quotation on 213.
103
Ibid., 279.
62
�frequencies of these oscillations are the roots of the characteristic equation of the system and,
Lagrange notices, if the roots are real and equal or imaginary, then arcs of circle appear and
the oscillations will increase steadily. “On the contrary, if the roots of this equation are all
real and unequal, the value[s] of [eccentricity and inclination] can not step over certain lim-
its”104 and it is easy to calculate exactly those extremes, which are now known as Lagrange’s
limits. Lagrange carries out the analysis for Jupiter and Saturn and finds, for instance, that
their eccentricities oscillates reciprocally, i.e., one reaches the maximum when the other
reaches the minimum, with a period of about 70,400 years. A perfectly analogous calculation
can be performed for the inclinations, which also exhibit an oscillatory evolution.
This analysis is relatively simple because Lagrange considers only two planets, thus the
characteristic equation has degree two and can be solved completely. But the problem be-
comes much more intricate for the inferior planets: Earth, Mars, Venus, and Mercury. The
high degree of the characteristic equation as well as the uncertainty in the evaluation of the
planetary masses make “more and more difficult to judge a priori the character of the roots.”
Lacking an exact response to the issue of stability, Lagrange confines himself to observe that
the roots found from the available data are “too different from each other for a small change
in the assumed masses to be able to make them equal, much less imaginary.”105 Thus, La-
grange can finally conclude his general statement on the stability of the solar system:
104
Ibid., 280.
105
Ibid., 316-317.
63
� [The] invariability of the mean distance as well as that of the mean motions which follows from
it, are the most interesting results of our analysis and the most remarkable features of the system
of the world. The planets, in virtue of their mutual attraction, change insensibly the form and
position of their orbits, but without ever going outside certain limits. The major axes remain
unalterable; at least the theory of gravitation implies only alterations that are periodic and de-
pendent on the positions of the planets, and indicates no secular variations, whether of the sort
that constantly increase, or of the sort that are simply periodic but independent of the positions
of the planets and with a very long period, like those which the same theory implies for the
other elements of the orbit, and which we have determined.106
Clearly, it is in Lagrange’s 1781-82 great memoir that the problem of the stability of the
solar system is first explicitly enunciated. Why did it emerge so late, if it was somewhat
implicit in Newton’s theory? The received view stresses the inadequacy of Newton’s pertur-
bation theory: the problem of stability was by far too difficult for Newton’s geometrical
methods. Had he been in possession of more powerful analytical techniques, he would have
tackled the issue and, most probably, solved it. There are two major difficulties with this
argument. First, the limits of Newton’s perturbation theory can explain why he didn’t solve
the problem, but can hardly explain why he never raised the question. Second, and perhaps
more important, we have seen that perturbation theory developed independently of the prob-
lem of stability, which was set as scientific puzzle only when the mathematical practices
required for its solution were finally developed. Far from being a driving force, the problem
106
Ibid., 344.
64
�of stability was a ‘retrocognition’107 of the lengthy process of refining and stabilizing the
mathematical practices of physical astronomy in the 1760s and 1770s. Only when mathema-
ticians reached a satisfactory understanding of how the perturbation techniques work, made
their notation more standardized and convenient, and improved their integration methods, it
became possible to extend these practices to the treatment of the solar system as a whole. In
other words, it was the awareness of having at hand powerful means of solution that made
possible to recognize that there was a problem.
These considerations suggest two points. First, math matters, but the relation between the
development of perturbation theory and the emergence of the problem of stability is much
more complex than previously acknowledged. Second, even if math matters, it cannot explain
everything. There were factors external to the world of mathematics that had an important
bearing on the transformation of stability into a scientific problem. Let me elaborate on these
two points.
The development of a more powerful perturbation theory became possible when the as-
sumption of the periodicity of the heavenly motions ceased to be regarded as a metaphysical
principle and started to be deployed as an effective tool to treat mechanical problems. As we
have seen, Euler’s groundbreaking innovations (the use of trigonometric series and the
method of variation of constants) extended the concept of periodicity and built it into the
mathematical fabric of perturbation theory. However, these innovations still contained flaws,
107
For this concept see Alan Lightman and Owen Gingerich, “When do Anomalies Begin?,” Science 255
(1992), 690-695.
65
�limitations, and obscurities. During the 1770s, Lagrange and Laplace refined the mathemat-
ical practices introduced by Euler and applied them extensively to a variety of open issues.
In this way, they improved the robustness and reliability of the theory and eventually pro-
duced the decisive advancements that made the stability problem treatable. Once the solution
was available, mathematicians could direct their attention to the most fundamental assump-
tion of their procedures, to wit the periodicity of celestial motions. In a nutshell, the problem
of stability emerged because (1) the assumption of periodicity became a tool, (2) it was inte-
grated into a flexible set of mathematical practices, (3) these practices became robust and
reliable through extensive deployment, and, finally, (4) the very assumption perturbation the-
ory relied on was scrutinized.
However, the step (1) of the previous argument exceeds the boundaries of mathematics.
If the founders of perturbation theory could use periodicity as a tool, the reason was that,
around mid-18th century, it became possible to think about order in nature in a novel way.
As we have seen, in Newton’s time natural order and divine order were tightly connected.
The universe was looked upon as a place ruled by God’s decrees. As a consequence, the
stability of the solar system was part of the theological discourse, rather than a possible field
of application of mathematics. The traditional link between divine and natural order estab-
lished by medieval theology started to crack at the end of the 17th century under the com-
bined action of multiple factors. I have no ambition to cover exhaustively this process here.
Rather, I will confine myself to some points particularly relevant for my argument.
First of all, in the second half of the 17th century time-honored beliefs related to the Scrip-
tures, the institutionalized religion, and the theological foundations of politics, society, and
66
�science underwent a deep historical and philosophical critique. The protagonists of this
movement were especially French and Dutch scholars, Spinoza being the most prominent
example, who developed the most radical implications of Cartesianism.108 Indefatigable crit-
ics of the cultural establishment, these radical philosophers revealed the tensions between the
new mechanical philosophy and the Cartesian compromise with the traditions of medieval
theology.
Second, from the beginning of the 18th century, new developments in economics, social
thoughts, and life sciences converged to suggest the idea that complex systems can manifest
a sort of self-organizing behavior. Many writers observed that financial cycles and societies
seemed to follow a logic completely independent of the goals and intentions of individuals
and tried to capture this tendency with the fortunate notion of “invisible hands”. The main
idea behind this metaphor was that the general behavior of systems constituted by several
108
See Jonathan I. Israel, Radical Enlightenment: Philosophy and the Making of Modernity 1650-1750 (Oxford:
Oxford University Press, 2002), Tad M. Schmaltz, Radical Cartesianism. The French Reception of Descartes
(Cambridge: Cambridge University Press, 2004), and Susan James, Spinoza on Philosophy, Religion, and Pol-
itics. The Theologico-Political Treatise (Oxford: Oxford University Press, 2012); on the medieval roots of Spi-
noza’s biblical and theological critique see, for instance, Funkenstein, Theology and the Scientific Imagination
(ref. 9), 213-221.
67
�independent elements resulted of mutually balancing actions and could therefore be de-
scribed by simple principles.109 One key consequence of the notion of self-organization is
that order in complex systems—be it political, social, economical, or natural order—was no
longer regarded as a transcendent phenomenon, but as something amenable to scientific in-
vestigation. Interestingly, when philosophers and intellectuals talked about self-organization,
they often had in mind images and instances derived from physical astronomy. For example,
the market model propounded by physiocrats such as Francois Quesnay, Pierre-Paul Le Mer-
cier de la Riviere, and Anne Robert Jacques Turgot relied explicitly on a notion of dynamic
equilibrium inspired by celestial motions:
This model of self-organization requires time to keep the system running, but then largely
removes the time variable from the equation. In ideal conditions such an equilibrium would
continue ad infinitum, perturbed cyclically but always temporarily. The system is dynamic but
self-correcting, and always returns to its initial state. Over time, such a self-organizing system
is in fact timeless.110
Finally, a third important element to bear in mind is the materialistic critique of the tradi-
tional pillar of natural theology, that is the “argument from design” according to which nat-
ural order leads immediately to a divine designer. In 1749, Denis Diderot devoted his Letter
on the Blind for the Use of Those Who See to argue that such an argument only takes its force
109
For an excellent historical analysis of the emergence of the concept of self-organization see Jonathan Sheehan
and Dror Wahrman, Invisible Hands. Self-Organization and the Eighteenth Century (Chicago: University of
Chicago Press, 2015).
110
Sheehan and Wahrman, Invisible Hands (ref. 109), 251.
68
�from an aesthetic approach to nature. Imagining a dialogue between a priest and the blind
mathematician Nicholas Saunderson on the latter’s deathbed, he pointed out that the timeless
impression of wonder before the natural world should be ascribed more to the peculiarities
of the visual experience than to an intelligent designer. A man like him, impaired in the use
of sight, was simply unmoved by that argument: “I have been condemned to spend my life
in darkness, and you cite wonders quite out of my understanding, and which are only evi-
dence for you and for those who see as you do. If you want to make me believe in God you
must make me touch Him.”111 Diderot’s larger point was one shared by many philosophes in
mid-18th century France: the connection between natural and divine order, so effective for
Newton, Clarke, and Leibniz, resulted from the illegitimate intertwining of physical, theo-
logical, and political discourses and had to be replaced by a proto-evolutionary theory of
nature.
Physical astronomy must thus be seen in dialogue with a larger cultural process of eman-
cipation from the traditional theological and metaphysical foundations of knowledge. Liber-
ated from the link with a transcendent source, order became a given of human and natural
phenomena and, as such, something to used as a tool or, alternatively, to study as a problem.
In this sense, perturbation theory did not merely put natural and divine order asunder, but
incorporated this new autonomous concept of natural order into its own practices and made
it symbolically manipulable and transformable for mathematical purposes. When Laplace
111
Denis Diderot, “Letter on the Blind for the Use of Those Who See,” in Diderot’s Early Philosophical Works,
ed. Margaret Jourdain (London: Open Court, 1916), 68-141, quotation on 109.
69
�reportedly answered Napoleon that he did not need the hypothesis of God, he was not just
indulging in a memorable quip: he was summarizing one of the deepest cultural changes of
his era.112
COMPLETING THE PICTURE
Lagrange’s proof of stability relied heavily on two conditions: the roots of the characteristic
equation must be real and unequal and the mean motions must be incommensurable. These
two conditions ensured the absence of arcs of circle. Although he managed to bring reason-
able arguments in support to the former, Lagrange essentially dismissed the latter as self-
evident and did not investigate more deeply into possible quasi-commensurabilities between
the mean motions. It was Laplace who grasped the meaning of this condition for the riddle
of the Great Anomaly. Laplace could study Lagrange’s paper immediately after its publica-
tion113 and on 23 November 1785 he announced at the Paris Academy his own contribution
112
This reference to Laplace’s witticism allows me to add an important word of caution. I am not claiming that
the interconnection of natural and divine order made the emergence of stability as a scientific problem impos-
sible. This would obviously be absurd. What I am claiming is that the idea of a transcendent foundation of
natural order discouraged the framing of the problem of stability. The reason, simply put, is that had the question
of stability been scientifically solved, one would have the uncomfortable problem of finding a place for God’s
action in an autonomous, self-organizing universe. This was exactly Newton’s prime fear and this is, ultimately,
the meaning of Laplace’s remark. We shall briefly see in the next section that 19th century natural theology
started from the proof of stability to carve a new space for God.
113
His letter to Lagrange on 11 February 1784 shows that Laplace read thoroughly the paper at an early stage,
see Lagrange, “Correspondance” (ref. 83), XIV, 129.
70
�to the theory of secular inequalities. Following Lagrange, he first discusses the general theory
and then, one year later, the analytical theory of Jupiter and Saturn. He begins with summa-
rizing Lagrange’s results and then he adds:
However, the uncertainty concerning many of these masses can lay down some doubt on this
result, and it is necessary to be assured by a method independent of all hypotheses, that, by
virtue of the mutual action of the planets, the eccentricities and the inclinations of their orbits
are always inconsiderable. I propose again to fulfill this objective in this memoir, and to estab-
lish in a general manner that the secular inequalities of the eccentricity and the inclination of
the orbits of the planets contain neither arcs of circles, nor exponentials; from which it follows
that, by virtue of the action of these bodies, their orbits flatten more or less, but never vary far
from the circular form and always conserve the same major axes.114
To be sure, Laplace’s point is slightly unfair. Although the uncertainty of the masses (of
the inferior planets) leaves doubts about the amount of the limits, Laplace seems to suggest
that Lagrange’s method fails to establish the nonexistence of secular inequalities. It is on this
incorrect base that he can present his general theory as a new “method independent of all
hypotheses,” which is, as we shall see in a moment, far from true. In fact, Laplace’s approach
deploys Lagrangean arguments, Lagrangean techniques and, finally, relies on the Lagrangean
idea of dealing with orbital elements rather than planetary coordinates. The new method con-
sists essentially in the combined use of the perturbing function and the integrals of motion,
particularly what we now call the conservation of energy. Laplace shows that, introducing
114
Pierre Simon Laplace, “Mémoire sur les inégalités séculaires des planétes et des satellites” (1784) OLP, XI,
49-92, quotation on 62.
71
�the perturbing function in the equations of motion and making some algebraic manipulations,
it is possible to obtain a complicated relation involving the masses, the mean motions, and
an integration constant.115
To simplify this relation, Laplace assumes without justification that certain functions are
periodic. If this is the case, one finds that the mean motions of the system, supposed inde-
pendently variable, must always add up to a fixed quantity, which depends on the total en-
ergy. As Laplace puts it: “thus, in supposing that the sequence of centuries leads to remark-
able changes in the semi-major axes […] of the orbits, they need always satisfy the preceding
equation in which f is invariable,”116 where f is the integration constant. By an analogous
argument, Laplace finds another integration constant c that constrains the variation of incli-
nation and eccentricity. The consequence is worded in the same fashion: “in supposing thus
that, after a considerable time, the eccentricities and the inclinations of the orbits undergo
remarkable changes, they need always satisfy the preceding equation in which the constant c
is invariable.”117 A simple manipulation of the first relation yields the invariability of the
mean motions, while the application of the Lagrange coordinates to the second shows that
inclination and eccentricity are bounded, from which one “can generally conclude that the
expressions of the eccentricities and the inclinations of the orbits of the planet contain neither
115
The clearest account of this method can be found in Laplace, Mécanique celeste (ref. 99) I, 346-351.
116
Laplace, “Les inégalités séculaires” (ref. 114), 68.
117
Ibid., 69.
72
�arcs of circles nor exponentials and that thus the system of the planets is contained within
invariable limits, at least as long as one regards only their mutual action.”118
Laplace’s argument is hardly more simple or general than Lagrange’s. True, he relaxes
some constrains on the variation of the mean motions, but his periodicity assumption is strong
and unjustified. All in all, his approach to stability does not improve dramatically Lagrange’s
either in methods, or in outcome. However, Laplace is acutely aware of the important role of
the incommensurability condition. In particular, he recognizes that the solar system manifests
cases of commensurable or quasi-commensurable mean motions. One example is the satel-
lites of Jupiter, which Laplace discusses briefly,119 but the most notable one is the Great
Anomaly. After stressing that his argument based on the energy conservation entails both the
correct sign and the correct ratio of the mean motions, Laplace enunciates his key intuition:
In examining the circumstances of the movements of Jupiter and Saturn, one easily perceives
that their mean motions are very close to be commensurable and that five times the mean mo-
tion of Saturn is almost equal to twice that of Jupiter; hence I concluded that the terms which,
in the differential equations of motion of these planets, have for argument five times the mean
longitude of Saturn minus two times the mean longitude of Jupiter, could become sizable be-
cause of the integrations, though they are multiplied by the cubes and products of three dimen-
sions of the eccentricities and inclinations of the orbits. Consequently, I have regarded this
118
Ibid., 92.
119
The satellites of Jupiter are in remarkable resonance with their primary. Laplace states, without proof, that
this case does not undermine the invariability of the mean motions. As a matter of fact, he is right, because this
is one of those cases in which commensurability in fact reinforces stability.
73
� difference as a very probable cause of the variation observed in the motions of Jupiter and
Saturn. The probability of this cause and the importance of this topic have pushed me to en-
deavor the long and painstaking calculation necessary to the verification.120
Laplace’s main idea is that if the commensurability of the mean motions generates diver-
gent terms, then a quasi-commensurability might generate sizable terms at higher orders of
approximation. The confirmation of this suspicion, however, required “long and painstaking
calculation.” The entire procedure occupies a lengthy paper, presented on 10 May and 15
June 1786, where Laplace proves that the Great Anomaly “far from being an exception to the
principle of gravitation, [it is] a necessary consequence of it, and presents a new confirmation
of this admirable principle.”121
Laplace’s paper is a masterpiece of computational ingenuity. He knows very well that a
full calculation of the perturbation is humanly impossible, therefore he uses multiple tech-
niques to select precisely those elements of the equations that could generate sizable inequal-
ities. His first brilliant move consists in using very effectively the concept of perturbing func-
tion to extract information about the effect of perturbation terms on the equations. Once he
has obtained simple expressions for the first order of the eccentricity and inclination, he en-
ters the unexplored territory of higher orders. Here comes another brilliant move. Laplace
knows that he must concentrate his attention on an angle depending on the difference between
the mean motions. Since the movements of Jupiter and Saturn are quasi-commensurable, the
120
Laplace, “Les inégalités séculaires” (ref. 114), 52.
121
Pierre Simon Laplace, “Théorie de Jupiter et de Saturne” (1786), OLP, XI, 95-239, quotation on 95.
74
�angle containing the difference between five times Saturn’s mean motion and twice Jupiter’s
will be very close to zero and, in successive integrations, will generate larger terms. The
problem is that at higher order one also obtains the squares of these angles and a maze of
cross products. But now Laplace’s computational genius comes to rescue. He manages to
find a rule to form the coefficients of the angle at any order and this rule allows him to de-
termine which coefficient will become sizable without actually performing the calculation.122
In this way, Laplace can establish that the quasi-commensurability of Jupiter and Saturn be-
comes relevant at the third order and he can perform the approximation on selected angles
only. At the end of a complex calculation, he finds a periodic correction for the longitude
equal to 47′ for Saturn and 20′ for Jupiter, whose period is about 877 years, i.e., 74 times the
mean motion of Jupiter and 30 times that of Saturn. The veil on the Great Anomaly had been
finally lifted. In the ensuing years, Laplace extended his approach to the satellites of Jupiter
and, more importantly, to the secular acceleration of the Moon thus bringing the work on the
stability of the solar system to a full circle.
THE EMERGENCE OF A NEW NARRATIVE
The story I have been telling over the foregoing sections challenges head-on the common
wisdom according to which it was Laplace who proved, in 1773 or in 1785, the stability of
the solar system. How did this narrative come about? An examination of research papers and
122
For an account of the details of this complicated procedure see Wilson, “The Great Inequality” (ref. 38),
251-253.
75
�textbooks written in late 1700 or early 1800 shows that astronomers and mathematicians
could correctly distinguish between Lagrange’s proof and Laplace’s addenda. For example,
Lalande, in the 1792 edition of his influential Astronomie, recalls that, while Lagrange “has
demonstrated rigorously that the major axes of the orbit at no point change by their mutual
attractions,” Laplace has applied this result to planetary motion up to the third order of ap-
proximation.123 Another notable example is Simon Denis Poisson, a central figure of the La-
placean school of mathematical physics. In a landmark paper in which he extends his mas-
ter’s analysis, Poisson states clearly that “Lagrange has given of [the problem of secular in-
equalities] a general and complete theory” and does not even mention Laplace’s contribution
to the stability of the solar system.124 On his part, in the mathematical papers, and particularly
in the Mécanique celeste, Laplace is very careful in crediting Lagrange of the rigorous proof
of stability. As a consequence, readers of the Mécanique celeste absorbed this narrative. In
reviewing the book for the Edinburgh Review, the mathematician John Playfair recollects a
historically accurate sequence of events leading eventually to the stability proof and stresses
the importance of Lagrange’s 1781 invariability result for the general theorem.125 Another
intelligent reader of the Mécanique celeste, Mary Somerville, recalls in the introduction of
123
Jerome Lalande, Astronomie, 3rd ed. (Paris: Didot, 1792), quotation on 478.
124
Simon Denis Poisson, “Memoire sur la variation des constantes arbitraires dans les questions de Mecanique,”
Journal de l’Ecole Polytechnique VIII (1809), 266-344, quotation on 267.
125
John Playfair, “Review of Laplace’s Mécanique celeste,” (1808) in The Works of John Playfair (Edinburgh:
Archibald Constable, 1822) VI, 261-330, see especially 289.
76
�her beautiful Mechanism of the Heavens that it was Lagrange’s theorem the key result to
exclude the “dreadful” consequences of secular inequalities.126
Examples could be easily multiplied to show that, way into the 19th century, astronomers
and mathematicians got the story quite right. Instead, the texts to look at to find the origin of
the present standard narrative are popular accounts and philosophical treatises. Probably the
oldest source of the myth is Laplace’s highly acclaimed Exposition du Système du Monde.
Although meant to be a handy compendium of physical astronomy, its style and the frequent
appearance of the first person gives the impression that the Exposition is in fact a summa of
its author’s own knowledge and feats. A case in point is Laplace’s recollection of the stability
theorem. In telling the story of the secular inequalities, he pinpoints his 1773 work on the
invariability of the mean motions as the key step and takes Lagrange’s 1776 paper as a mere
refinement. Next, when dealing with the stability theorem, Laplace presents his own work in
1785 as the real core of the theorem:
I have succeeded in demonstrating that whatever be the masses of the planets, in as much as
they all move in the same direction, in orbits of small eccentricity, and little inclined to each
other, their secular inequalities will be periodic, and contained within narrow limits, so that the
planetary system will only oscillate about a mean state, from which it will deviate but by a very
small quantity.127
126
Mary Somerville, Mechanism of the Heavens (London: Murray and Highley, 1831), see xiv-xv.
127
Laplace, Exposition (ref. 99), 226.
77
� Laplace’s decision to highlight his own role in the history of the stability problem has
probably more to do with the audience of the book than with the medium of popularization.
Always an indefatigable self-promoter, Laplace was engaged in becoming France’s foremost
scientific authority not only in the eyes of his peers, but also in those of administrators and
policy-makers.128 His followers contributed to propagate the narrative of Laplace’s stability
theorem. One key example is Francois Arago’s immensely influential course of popular as-
tronomy. Held uninterruptedly from 1813 to 1846 and open to the general public, the course
made astronomy part of popular culture and, after its posthumous publication, continued to
impress French minds for decades. At the beginning of the fourth volume, Arago reviews the
development of the stability issue and frames the narrative we often find today. Newton’s
gravitation theory led naturally to the problem of stability and “never did a greater philosoph-
ical question present itself to the curiosity of men.” Laplace is the only hero of this titanic
quest: he “attacked it with boldness, constancy and good fortune.”129 Again, the key steps are
the paper of 1773, subsequently refined by Lagrange and Poisson, and the memoire of 1785,
which places stability on firm ground. The conclusion is almost metaphysical: “Laplace’s
magnificent work, of which I have just given a short account, will not ever again allow, at
least in our solar system, to consider Newtonian attraction as a cause of disorder.”130 It is
interesting to note that Arago’s influence went well beyond France and reached the educated
128
On Laplace’s career see Gillispie, Laplace, (ref. 69) and Roger Hahn, Pierre Simon Laplace. A Determined
Scientist, (Cambridge, MA: Harvard University Press, 2005).
129
François Arago, Astronomie Populaire (Luxembourg: Legrand, Pomey et Crouzet, 1854), IV, 20.
130
Ibid., IV, 22.
78
�bourgeois of many countries. For instance, a summary of his account of Laplace’s work was
published in a journal for a sophisticated readership in the United States.131 In this way, the
standard narrative was appropriated by scientific amateurs, learned middle-class readers, and
students.
Another important vector of dissemination for the standard narrative was, surprisingly
enough, philosophical debates on the meaning of the new science. The reason was that La-
place was very effective in enunciating explicitly the conditions for stability thus providing
the ground for discussing the cosmogonical question. In a short, but very clear paper pre-
sented in 1787, Laplace clarified a point which had remained disguised in 1784:
As for the stability of the planetary system, I have proven in our Memoirs for the year 1784
that as long as the planets always move in the same sense and their orbits are nearly circular
and little inclined to one another, the eccentricities and inclinations of these orbits are always
contained within narrow limits, and thus the system of the world makes only oscillations around
a mean state from which it never strays more than a small quantity.132
These peculiar conditions—small eccentricity and inclination, same sense of revolution—
reopened the debate on the relation between natural and divine order. Physical astronomy
had pushed a godless notion of order toward a proof of stability, but God could still have a
131
François Arago, “Astronomical Discoveries of Laplace,” The Anglo American, a Journal of Literature, News,
Politics, the Drama, Fine Arts, Etc. (1843-1847) 4 (1844), 59-61.
132
Pierre Simon Laplace, “Memoire sur les variations seculaires des orbites des planetes” (1787) OLP, XI, 295-
306, quotation on 296.
79
�say in the selection of the essential conditions. Playfair, for example, grasped this point very
firmly:
Now, these conditions are not necessary; they may easily be supposed different; any of them
might be changed, while the others remained the same. The appointment of such conditions
therefore as would necessarily give a stable and permanent character to the system, is not the
work of necessity; and no one will be so absurd as to argue, that it is the work of chance: it is
therefore the work of design, or of intention, conducted by wisdom and foresight of the most
perfect kind.133
Laplace agreed that the special conditions of the solar system cannot possibly be the effect
of pure chance, but argued that some physical process should be the reason. He suggested
that the solar system originated from a rotating nebula, which progressively generated the
Sun and the planets. Because of this common origin, the planets possess the same direction
of revolution. The nebular hypothesis constituted one of the most powerful weapon for the
supporters of positivist philosophy.134 Meanwhile, on the other side of the Channel, the up-
holders of Natural Theology viewed in Laplace’s work the opportunity to revitalize the old
argument from design. If the favorable conditions of the solar system were not chancy, they
133
Playfair, “Review” (ref. 125), 319.
134
On the debate stirred by the nebular hypothesis see Simon Schaffer, “The Nebular Hypothesis and the Sci-
ence of Progress,” in History, Humanity and Evolution, ed. James R. Moore (Cambridge: Cambridge University
Press, 1989), 131-164 and Sam S. Schweber, “Auguste Comte and the Nebular Hypothesis,” in In the Presence
of the Past. Essays in Honor of Frank Manuel, ed. Richard T. Bienvenu and Mordechai Feingold (Dordrecht,
Kluwer, 1991), 131-191.
80
�suggest the hand of an intelligent designer. William Whewell was among those who pursued
most intensely this point. He argued energetically that the very specificity of the circum-
stances that make the solar system stable reveals the act of a provident creator:
Now is it probable that the occurrence of these conditions of stability in the disposition of the
solar system is the work of chance? Such a supposition appears to be quite inadmissible. […]
And these circumstances, which appear to be, each in particular, requisite for the stability of
the system and the smallness of its disturbances, are all found in combination. Does not this
imply both clear purpose and profound skill?135
The proof of the stability of the solar system had a huge cultural impact and entered several
debates involving positivist philosophy, natural theology as well as social and political re-
formism. But the participants of these debates mostly interiorized the Exposition version of
the story and his convenient formulation of the conditions of stability. Laplace provided them
with the essence of the matter, saving them all the intractable mathematical complications.
In this way, Laplace was progressively associated with the stability theorem and the standard
narrative established itself.
135
William Whewell, Astronomy and General Physics Considered with Reference to Natural Theology (Lon-
don: William Pickering, 1833), 165-166.
81
�CONCLUSION
In his third travel, Gulliver visits Laputa, a flying city populated by scientists whose only
interests are mathematics, music, and politics. Apparently, their worst fears concern the evo-
lution of the cosmos: “Their Apprehensions arise from several Changes they dread in the
Celestial Bodies. For Instance; that the Earth by the continual Approaches of the Sun towards
it, must in Course of Time be absorbed or swallowed up.” The target of Swift’s prose is,
clearly enough, the mathematical community of his time, particularly Isaac Newton. His sat-
ire addresses the peculiar mixture of science, politics, and theology that characterized the
thought of Newton and his followers. By ridiculing the preoccupations for the fate of the
universe, Swift is attacking not only the connections between astronomy and Apocalypse,
but also the use of science for political and theological programs.
Gulliver’s Travels was published in 1726, one year before Newton’s death, when the link
between natural and divine order was still strong but on the verge of declining. After Newton,
the inverse-square law became one of the fundamental laws of nature and, in physical astron-
omy natural order was epitomized by the model of periodic elliptical orbits. In the late 1740s,
this concept of natural order was encapsulated in new, powerful, and extraordinarily flexible
mathematical practices. The use of trigonometric series and the method of variation of con-
stants codified symbolically the idea that all heavenly motions are ever-changing ellipses and
enabled mathematicians to manipulate and transform this idea into workable equations of
motion. Progressively, the concept of natural order was separated by divine order, a process
that was taking place in mathematics as well as in other ambits of the Enlightenment culture.
In the late 1760s and throughout the 1770s, Lagrange elaborated perturbation theory with the
82
�goal of making it more robust, reliable, and accessible. The ultimate result of this laborious
work was the emergence of solution conditions for the problem of stability.
This story conveys some important methodological points. It is usually assumed that sci-
entific research is dominated and directed by well-posed problems to be resolved by certain
techniques. Kuhn elevated this idea to the notion of paradigm, whose main function is pre-
cisely to define problems, to ensure that they are solvable, and to provide the conditions under
which they should be considered as solved. More interestingly, the development of physical
astronomy after Newton is viewed by Kuhn as the ‘paradigmatic’ example of normal science:
“Euler, Lagrange, Laplace, and Gauss all did some of their most brilliant work on problems
aimed to improve the match between Newton’s paradigm and observation of the heavens.”136
Thus, according to Kuhn, Newton set the puzzles and the rules of the game, while his suc-
cessors tried to solve the former playing by the latter. This is basically the same idea under-
lying the standard narrative on the stability theorem.
But there are several difficulties with this problem-oriented approach. First, it has been
argued that the ‘Newtonian paradigm’ was not established by Newton, but emerged slowly
out of the competition between several mechanical programs.137 In fact, the work of Euler in
136
Thomas S. Kuhn, The Structure of Scientific Revolutions, 2nd ed. (Chicago: University of Chicago Press,
1970), quotation on 32.
137
See, for example, Clifford Truesdell, “A Program Toward Rediscovering the Rational Mechanics of the Age
of Reason,” in Essays in the History of Mechanics (New York: Springer, 1968), 85-137 and Helmut Pulte,
“Order of Nature and Orders of Science,” in Between Leibniz, Newton, and Kant, ed. Wolfgang Lefevre (Dor-
drecht: Kluwer, 2001), 61-92.
83
�the 1750s and Lagrange in the 1770s can still be regarded as steps toward the definition of
the modern notion of Newtonian paradigm. Second, we have seen that, far from guiding as-
tronomical research, the stability problem was co-created with its own solution. Only when
perturbation theory reached a certain level of robustness, it became possible to ‘retro-cog-
nize’ that it allowed the definition of a stability problem as well as the conditions under which
it could be considered as solved. To be sure, there is a grain of truth in Kuhn’s statement.
Perturbation theory from the late 1740s to the 1780s, was mainly a careful (and at times
tedious) exploration of the potentiality of Newton’s gravitational theory. But what gets lost
in Kuhn’s characterization in terms of paradigm is the impact of the new mathematical prac-
tices and the reflexive cognitive process that they made possible.
These considerations lead to another, larger, point. It is commonplace to ascribe to math-
ematical practices what one can call a connecting function. They are seen to establish a log-
ical and mathematical connection between theoretical posits and their theoretical or observa-
tional consequences. This function is epistemically neutral: in forming logical links, mathe-
matical practices do not add anything to the epistemic content of the original posits. They
only unfold what is already implicitly contained in the starting point. However, recent histo-
riography has pointed out that mathematical practices can play a crucial epistemic role in
determining the mindset of the practitioners or in the way in which theories are appropriated
84
�and disseminated.138 The previous discussion adds a further dimension. To understand how
stability became an object of inquiry and how scientific knowledge could eventually be gen-
erated about it, one needs to look at the way in which certain epistemic content, to wit a
concept of natural order and Newton’s gravitational posits, was integrated in the mathemati-
cal practices and made workable through them. In this sense, mathematical practices also
exhibit a performative function: they might play an active role in defining problems, in fram-
ing contexts of applications, and in refining concepts.139 The case of the stability of the solar
system exemplifies the performative power of mathematical practices and suggests that they
are a crucial site for the generation of theoretical knowledge.
138
Prime examples of this re-evaluation of mathematical practices are Andrew Warwick, Masters of Theories
(Chicago: University of Chicago Press, 2003) and David Kaiser, Drawing Theories Apart: The Dispersion of
Feyman Diagrams in Postwar Physics (Chicago: University of Chicago Press, 2005).
139
On the notion of performativity applied to theories see, for example, Donald MacKenzie, An Engine, Not a
Camera. How Financial Models Shape Markets (Cambridge, MA, MIT Press, 2005), 1-25.
85
�


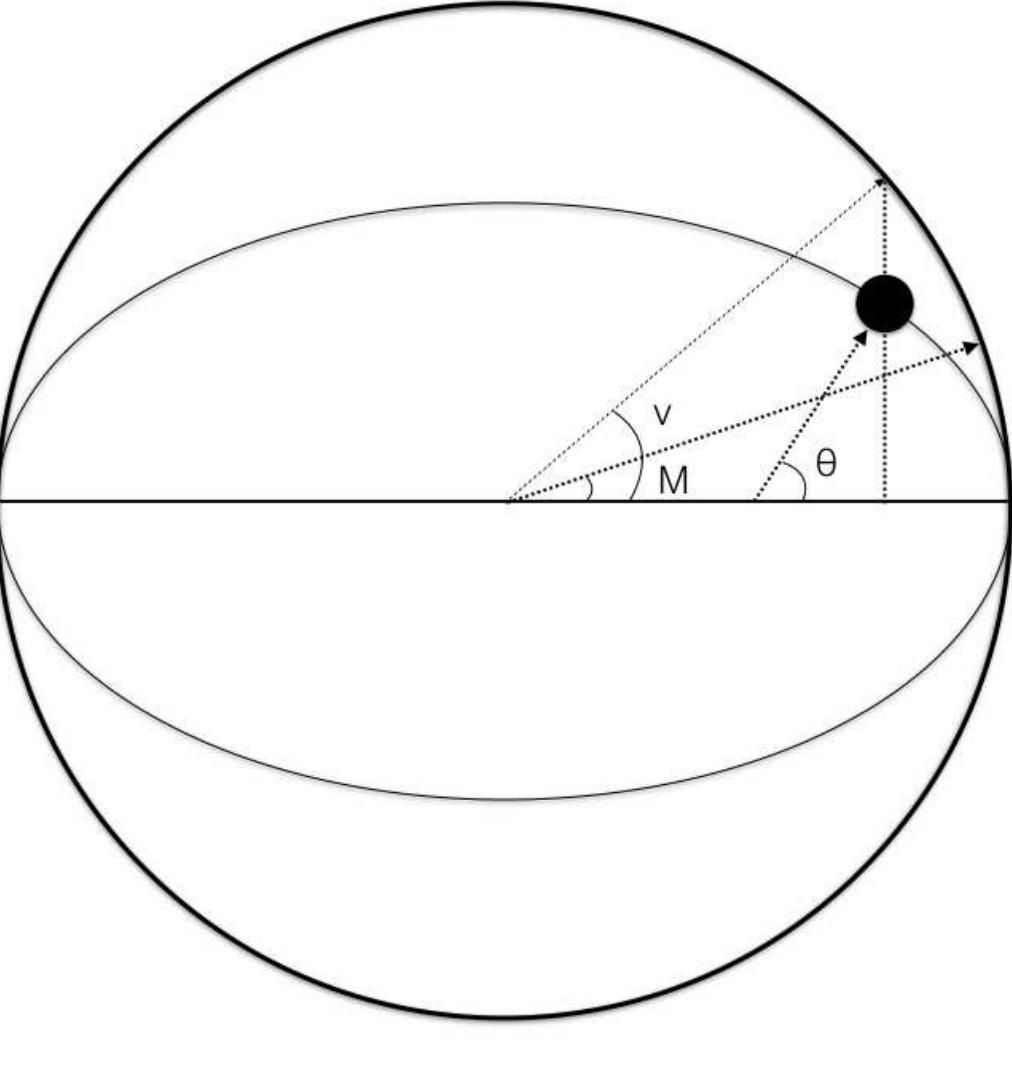
 Massimiliano Badino
Massimiliano Badino
