Introduction

Fluctuations in groundwater level (GWL) can be used to evaluate groundwater stability and flow as well as the characteristics of the aquifer. Moreover, groundwater is the main source of farmland irrigation in major agricultural regions. Agricultural water managers assess whether groundwater is needed during sowing season and how much is likely to be provided (Barlow and Clark 2011; Dyer et al. 2015; Kebede et al. 2014). Although most government agencies collect GWL data once or twice a year in major agricultural areas, this is not sufficient for short-term studies. Therefore, it is necessary to achieve acceptable prediction accuracy of GWL variations when previous information is not available and the computational sources are limited. It is well known that the dynamic variation in GWL is influenced by meteorological phenomena, urbanization, tidal effects, and land subsidence (Khaki et al. 2015). Of these, such meteorological parameters as atmospheric pressure, frost, precipitation, and evapotranspiration are considered important indicators of fluctuations in GWL.

Models to simulate groundwater can be classed into two main groups: physical models and data-driven models. For physical models, an appropriate synthesis of the parameters of the aquifer is used to determine the spatial variation in underground space. This information is challenging to obtain even through expensive on-site surveys, which further increase computational cost. Therefore, the physical domain needs to be partitioned to obtain a numerical solution (Taormina et al. 2012). An appropriate alternative to the physical model is the data-driven model, which can provide accurate predictions without a costly calibration time when data are insufficient and the physical mechanism is not the focus of research (Mohanty et al. 2015). Artificial neural network (ANN)-based techniques and the support vector machine (SVM) are data-driven models treated as standard nonlinear estimators and can overcome the limitations of the physical model (Behzad et al. 2010).

In groundwater hydrology, ANNs have been used in such applications as groundwater level prediction (Emamgholizadeh et al. 2014; He et al. 2014; Khaki et al. 2015). However, it is known that ANN models incur the disadvantages of local minima and problems of overfitting. The SVM can overcome these drawbacks (Hosseini and Mahjouri 2016). Comparative studies on the SVM and the ANN have been performed in the context of GWL prediction. Behzad et al. (2010) compared the SVM and ANN for predicting transient GWL under variable pumping and weather conditions. Yoon et al. (2011) developed and compared two time-series forecasting models using ANN and SVM and applied them to forecast GWL fluctuations in a coastal aquifer recharged from precipitation and tidal effects. Yoon et al. (2016) compared the recursive prediction performance of the SVM and ANN for the long-term prediction of GWL and concluded that SVM is a better substitute for ANN in terms of accuracy and robustness for the prediction of GWL fluctuation.

Although SVM is superior to ANN in reflecting the dynamic variation in GWL, it takes more time because of trial and error (Raghavendra and Deka 2014). It is also sensitive to outliers and redundant data (Suykens et al. 2002). On the contrary, results of the prediction of random forest (RF) are unaffected by outliers and redundant data (Rodriguez-Galiano et al. 2014). Comparative studies on RF and SVM have been carried out from different perspectives. For example, Pal (2005) compared RF with SVM in terms of classification accuracy, training time, and user-defined parameters. They were also compared on four criteria in mineral prospectivity modeling (Rodriguez-Galiano et al. 2015). In these case studies, the authors concluded that the RF model exhibited stronger predictive capabilities and higher robustness, with a lower complexity of parameterization and a shorter training time for optimization than the SVM.

RF has been widely used in surface and ground water hydrology. Many studies have applied RF to study groundwater from different aspects, such as its vulnerability to nitrate pollution (Rodriguez-Galiano et al. 2014), the dissolution of organic nitrogen in it (Wang et al. 2016), and the potential mapping of groundwater (Rahmati et al. 2016). Moreover, the RF model has been compared with the SVM in terms of surface water level prediction (Li et al. 2015). However, no study to date has applied RF to the prediction of GWL owing to low-dimensional input features.

Breiman (2001) introduced a random forest algorithm (Forest-RC) that used linear combinations of input variables when dealing with low-dimensional input data. Although Breiman (2001), Hamza and Larocque (2005) and Moudani (2013) have shown that Forest-RC yields better results than those obtained with no linear combination, there are five key limitations to this approach:

  1. 1.

    The extended number of dimensions in Forest-RC is limited when the original data contain few dimensions of feature.

  2. 2.

    The original feature information, which is important for regression and has a certain impact on its results, is removed by Forest-RC.

  3. 3.

    The information in the new feature varies with the value of L, which is the number of selected variables that are combined. Furthermore, it directly affects the construction of the decision trees. Experiments have shown that different values of L lead to different generalization capabilities (Luo et al. 2016).

  4. 4.

    A fixed value of L is contrary to randomness, which is introduced by choosing training samples randomly and using a random subset of all features as the set of splitting rules. The value of L must be adjusted for different prediction horizons for GWL, which limits the versatility of the Forest-RC algorithm in practical applications.

  5. 5.

    Forest-RC uses orthogonal (i.e., axis-aligned) decision trees that only recognize axis-parallel splits of the feature space and lead to poorer performance of trees than oblique decision trees. Zhang and Suganthan (2015) showed that oblique random forests achieved better performance than their conventional axis-parallel counterpart in computation time and classification accuracy.

Based on the above issues, in this paper, we propose a method of GWL modeling based on canonical correlation forests with a combination of random features (CCF-CRF) that expands the low-dimensional feature vector space to high-dimensional space and uses canonical correlation components for oblique splits. A comparison of performance among CCF-CRF, random forest regression (RFR) algorithm, and least squares support vector regression (LS-SVR) was conducted and showed that CCF-CRF can provide the most accurate short-term GWL forecasts. For this purpose, we chose the monitoring well Guxian along the groundwater source for the Daguhe River for a case study.

Materials and methods

Random forest regression algorithm (RFR)

Based on classification and regression trees (CART), random forest (RF) builds a forest from bootstrap samples of observed data. Having generated multiple decision trees in the process of training, RF is designed to generate an output by majority vote (for classification) and the average of the single-tree method (for regression) (Breiman 2001). GWL as the output of this prediction is a continuous variable. Thus, we focus on the regression model of RF.

A regression tree (RT), where each non-leaf node contains a set of decision rules and each leaf node is the outcome of a prediction, is a form of decision tree (DT) (Quinlan 1993; Rodriguez-Galiano et al. 2014).

The two user-defined parameters of RF are B, the number of trees in the forest, and D, the number of features used to split the nodes. The default value of B is 500, but is reset according to application. One third of the variables for the regression task are set to the default value of D.

Steps of the RF regression algorithm are as follows (for full details, see Breiman 2001):

  1. 1.

    Different bootstrap samples Xi (i = bootstrap iteration) are randomly drawn from the original dataset X. Two-thirds of the samples are included in a bootstrap sample and one third as the out-of-bag samples. Each tree is constructed to correspond to a particular subset of the bootstrap.

  2. 2.

    At a node in each tree, a new split is randomly selected from all indices, and the input variable with the lowest mean square error (MSE) is chosen as the splitting criterion of the regression tree.

  3. 3.

    The data splitting process in each internal node is repeated according to the above steps until all randomized trees have been grown and a stop condition is reached.

  4. 4.

    The final results of regression can be calculated as follows, where B stands for the number of trees in the forest and Tb represents each tree:

    $$\hat{y}(x_{i} ) = \frac{1}{B}\sum\limits_{b = 1}^{B} {T_{b} (x_{i} )} .$$
    (1)

Least squares support vector regression (LS-SVR)

An extension of the standard support vector regression (SVR) (Smola et al. 2004; Vapnik 1995) is least squares support vector regression (LS-SVR) (Pelckmans et al. 2002; Suykens and Vandewalle 2000). LS-SVR is a series of deformations that can replace the quadratic programming problem with the linear equation problem. The calculation can thus be made easier, and the time needed to obtain a solution can be effectively reduced.

The basic principle of LS-SVR is introduced in this section (Suykens and Vandewalle 2000). The training sample set was assumed to be \(\{ X_{i} ,Y_{i} \}_{i = 1}^{N}\), where \(X_{i} \in R^{k}\) are the input data and \(Y_{i} \in R\) the output data. The relationship between the input and output data is as follows:

$$Y(X) = \sum\limits_{i = 1}^{N} {\alpha_{i} G(X,X_{i} ) + b}$$
(2)

where \(G\) is a kernel-based function and \(\alpha_{i}\) and \(b\) are parameters of the regression. The primary method of LS-SVR involves converting the parameter estimation problem into the following quadratic programming problem:

$$\mathop {\hbox{min} }\limits_{\alpha ,b,e} \frac{1}{2}\alpha^{T} \alpha + \frac{\gamma }{2}e^{T} e$$
(3)
$${\text{s}} . {\text{t}} .\;\,Y_{i} = \sum\limits_{j}^{N} {\alpha_{j} G(X_{i} ,X_{j} )} + b + e_{i} ,\;i = 1, \ldots ,N$$
(4)

\(\gamma \in R^{ + }\) is a penalty factor, \(e_{i} \in R\) is the bias term, G is the radial basis function (RBF), a kernel function that is the best choice for researchers because it has higher accuracy and reliability than other kernel functions (Raghavendra and Deka 2014), and \(\alpha_{i}\) and \(b\) are parameters of the regression. With \(\hat{Y} = (Y_{1} ,Y_{2} , \ldots ,Y_{N} )^{T} \in R^{N}\) and \(1_{N} = (1,1, \ldots ,1)^{T} \in R^{N}\), the solutions are given by

$$\left[ {\begin{array}{*{20}c} {\varOmega + \frac{{I_{N} }}{\gamma }} & {1_{N} } \\ {1_{N}^{T} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \alpha \\ b \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\hat{Y}} \\ 0 \\ \end{array} } \right]$$
(5)

where \(\varOmega_{i,j} = G(X_{i} ,X_{j} )\) is the kernel matrix and \(I_{N}\) the identity matrix of order \(N\).

Canonical correlation forests with a combination of random features (CCF-CRF)

The algorithm improves the predictive performance in two respects:

(1) the use of a combination of random features that introduces more randomness to build the decision tree, and (2) the use of canonical correlation analysis (CCA) to generate candidate hyperplane splits and projection bootstrapping to construct ensembles of the oblique decision tree.

  1. 1.

    A combination of random features

Two ingredients involved in the generalization error for random forests: the strength of a predictor in the forest and the correlation between trees (Breiman 2001). When the strength is fixed, the lower the correlation coefficient, the smaller the generalization error. Luo et al. (2016) proposed that one solution that reduces the correlation coefficient involves expanding the low-dimensional feature vector space to a high-dimensional space.

The original RF method can handle cases with only a few inputs. The only viable solution to this problem is to increase the dimensionality of the feature space, which can be done by creating linear combinations of input features. Forest-RC (Breiman 2001) is one such method and was introduced to define more features by using random linear combinations of input variables.

In Forest-RC, NL features are selected randomly from the original features at each node and linearly combined together with a random number uniformly distributed in the interval [− 1, 1]. We thus get the variable names V, whose formulation is as follows:

$$V = \sum\limits_{i = 1}^{L} {K_{i} V_{i} ,\;\;K_{i} } \in [ - 1,1]$$
(6)

Thus, more features are defined by taking random linear combinations of the input variables, and the nodes are split using the optimal predictive variable among these new features.

As mentioned in the “Introduction” section, Forest-RC has five defects. To overcome them and improve the predictive performance of the ensemble, this paper proposes an algorithm called canonical correlation forests with a combination of random features (CCF-CRF). The value of L induces randomness to enable the feature space to contain a greater number of novel and different features. The original m-dimensional feature space is extended to n-dimensions, and this relationship is described by the following equation:

$$n = \sum\limits_{i = 1}^{m} {C_{M}^{i} } .$$
(7)

It is clear from Eq. (7) that the new n-dimensional feature space not only contains the original feature space, but also contains the linear combination of arbitrary features. CCF-CRF is thus an approach that creates a higher-dimensional feature space than that of Forest-RC and RFR. The processing of the CCF-CRF algorithm is described in detail in Fig. 1.

Fig. 1
figure 1

Description of CCF-CRF algorithm

Full size image

CCF-CRF, where the split at each node is based on completely random linear combinations of features instead of a single one, has a lower probability of choosing the same attribute for each node, which reduces the similarity of the decision trees. To reducing the correlation coefficient and the generalization error, more randomness is introduced into the building of individual regression trees by the CCF-CRF algorithm.

  1. 2.

    CCA and projection bootstrapping

Canonical correlation analysis (CCA) (Hotelling 1936) is used to calculate pairs of linear projections to maximize the correlation coefficient between matrices in a co-projected space. In the first step, features λ appearing in Algorithm 1 are sampled without replacement from the input feature set Fs, which is generated from the process in part 2.2 of this algorithm. In the next step, a new training set {X′, Y′} is selected from {X(:,λ), Y} using the bootstrap sampling technique. CCA coefficients relating the features to the outputs are then calculated based on the new training set. The canonical coefficients Φ corresponding to X are used to generate the new features, which are obtained by projecting the original features into the canonical component space. Furthermore, the function FINDBESTSPLIT obtains the best split ξ by calculating the maximum information gain (Quinlan 1986).

From the above analysis, it is clear that the main difference between RF and CCF-CRF is that the latter uses CCA to analyze the relationship between the output and the features and then splits the nodes using an exhaustive search in the projected space.

Study area and data processing

Study site and data description

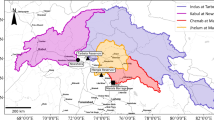
The study site was located at the groundwater source field of Daguhe River in Qingdao, China. The monitoring well Guxian, located in the northwest of the study area, was used as an example to verify the effectiveness of the CCF-CRF model. The groundwater source field of Daguhe River is among the important public drinking water sources in Qingdao. It is located in the northwest of the city and covers an area of approximately 4600 km2, with the temperature ranging from − 3.3 °C in January to 25.3 °C in July and average annual precipitation of 625.3 mm. The geographical position of the site is shown in Fig. 2.

Fig. 2
figure 2

Map of situation of the studied site (Guxian Station)

Full size image

Figure 3 shows a typical geological profile along section a–a′ nearby Guxian. The major aquifer systems of the study site were constituted by quaternary alluvium and diluvium, consisting of unconsolidated gravel, sand, silt, and clay with a width of 5–7 km. The maximum width was more than 10 km, and the thickness ranged from 10 to 20 km. The aquifer system was discretized vertically into two layers. There were particles of small size in layer 1, which was covered with silty clay, and their width ranged from 2 to 5 km. Layer 2 was stocked with sand and gravel, with larger particle sizes with a thickness ranging from 4 to 8 km. The bottom could be regarded as aquiclude composed of clay rock and sandstone and is also known as the lower confining bed.

Fig. 3
figure 3

Simple geological profile along the section a–a′ near by Guxian well

Full size image

In a majority of the area, the rainy season peaked in May through July. The most obvious characteristics of this area were the vegetation cover and the absence of a significant variation in topography. The depth to the groundwater was small, with a thin silt-like clay layer in this area, which created conditions favorable for rainfall infiltration. Precipitation was thus the primary and most critical variable affecting short-term fluctuations in groundwater level within the study site.

The precipitation in millimeters and temperature data in Celsius were obtained from a meteorological station located near the Guxian GWL station. Daily data for the groundwater level for the site were collected from a remote monitoring system designed to provide accurate scientific basis for the monitoring, exploitation, and protection of groundwater from the Daguhe River groundwater source field. Daily GWL values used in this modeling were the averages of two measurements per day, whereas the corresponding daily precipitation value was the total precipitation measured over a 24-h period, and the corresponding daily minimum temperature was the minimum value of all observations within a day.

From Fig. 4, it is clear that the lowest GWL (during the study period) obtained in July 2013 and 2014, with warmer months yielding the lowest GWL. This can be attributed to higher evaporation rates owing to higher temperatures in the summer, which motivated higher groundwater extractions and soil-moisture deficits. On the contrary, highest GWL occurred in spring under natural conditions because recharge was relatively high and groundwater pumping extraction remained relatively low.

Fig. 4
figure 4

Time-series plot collected at Guxian studied site

Full size image

Data preprocessing and performance criteria

The RFR, LS-SVR, and CCF-CRF models for GWL forecasting at the Guxian well station were written in MATLAB. The applied data were gathered from January 1, 2013, to November 19, 2014, at the Guxian well. For each dataset, 66.5% of the data were selected as the initial training samples set T, and the remaining 33.5% were used as test samples. To calibrate the parameters of the LS-SVR model, the training samples set were divided into two parts: a training set and a calibration set. In the former, system behavior had been learned and the correlated patterns between the input dataset and the target values identified by LS-SVR. In the latter, the optimal model parameters were determined under the rule of minimizing error through a trial-and-error process. In the testing stage, the performance of a fully specified predictor was assessed on criteria for model performance. However, a separate calibration set was not needed for the RF to obtain an unbiased estimate of the test set error because out-of-bag estimation is the internal cross-validation of the training set and a good tool for optimizing the parameters.

Before the data were treated by these three models, all input and output data in the training process were normalized using the mean (Xmean) and maximum (Xmax) values, as described in Eq. (8), so that the variables (X) in the training and testing datasets ranged from − 1 to 1. In Eq. (8), Xnorm, X, Xmean, and Xmax represent the normalized value, the real value, the mean value, and the maximum value, respectively:

$$X_{\text{norm}} = \frac{{X - X_{\text{mean}} }}{{2X_{\rm max } }}.$$
(8)

The root-mean-square error (RMSE), the mean absolute error (MAE), and the correlation coefficient (R) are usually employed as evaluation metrics of the model used in this study. The RMSE is a standard metric for model error and represents the degree of linear relationship between the observed GWL values and the forecasted values. As the errors are squared before they are averaged, it is very sensitive to large errors in a set of measurement data. The MAE is another useful method that uses the deviation between the forecasted values and the actual values to reflect the accuracy of the system. Equation (11) represents the MAE. The predictive capability of the model was evaluated by RMSE and MAE from different points of view. Our analysis indicates that MAE is a good measure of overall error in the training and testing sets, and RMSE measures the goodness of fit relevant to high values. The best fit between the observed and estimated values would have been R = 1, RMSE = 0, and MAE = 0. These parameters were calculated by using the following equations:

$$R = \frac{{\sum\nolimits_{i = 1}^{n} {(Q_{i}^{\text{o}} - \bar{Q}^{\text{o}} )(Q_{i}^{\text{p}} - \bar{Q}^{\text{p}} )} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {(Q_{i}^{\text{o}} - \bar{Q}^{\text{o}} )^{2} } \sum\nolimits_{i = 1}^{n} {(Q_{i}^{\text{p}} - \bar{Q}^{\text{p}} )^{2} } } }}$$
(9)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {(Q_{i}^{\text{p}} - Q_{i}^{\text{o}} )^{2} } }$$
(10)
$${\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {Q_{i}^{\text{p}} - Q_{i}^{\text{o}} } \right|}$$
(11)

where n is the number of input samples, \(Q_{i}^{\text{o}}\) and \(Q_{i}^{\text{p}}\) are the observed and predicted GWLs at the ith time step, respectively, \(\bar{Q}^{\text{o}}\) and \(\bar{Q}^{\text{p}}\) represent the mean values of the observed and predicted GWLs, respectively.

Results and discussion

Comparison of RFR, LS-SVR, and CCF-CRF to determine the best model

The performance of the original RFR, LS-SVR, and CCF-CRF models is compared in Fig. 5 for forecasting variations in 1-, 3-, 5-, 7-, and 10-day groundwater levels at the Guxian site. All performance evaluation measures of the CCF-CRF model, including R, RMSE, and MAE, are shown in red. The same input structures and prediction horizons as in the CCF-CRF model were introduced to the LS-SVR model, whereas the RFR model had three driving factors: temperature, precipitation, and previous GWLs. The number of decision trees (B) was set to 100 because the differences in computation time were more obvious, but those in accuracy were small when the number of decision trees was more than 100 (Rodriguez-Galiano et al. 2012). The default value of parameter D was 1/3 of the total number of variables.

Fig. 5
figure 5

The performance comparison of the original RFR model, LS-SVR model, and CCF-CRF model for forecasting the 1-, 3-, 5-, 7-, and 10-day-ahead groundwater level variations at Guxian site

Full size image

According to Fig. 5, the LS-SVR model yielded the best R, RMSE, and MAE scores in 1-day prediction. However, as the lag time of the forest increased, CCF-CRF gradually began to exhibit performance superior to that of the RFR and LS-SVR models in terms of overall trend. Furthermore, Fig. 5 shows that RFR outperformed LS-SVR for long-term predictions primarily because it split each node using only the best feature from a random subset of features. This operation can be seen as internal feature selection with no equivalent in the LS-SVM. Above all, it can be concluded that the CCF-CRF model was the most efficient for daily groundwater forecasting for two reasons. First, the split at each node was based on completely random linear combinations of features instead of a single one and had a lower probability of choosing the same attribute for each node, which reduced similarity among the decision trees. Second, as an alternative to the bagging technique (Breiman 1996), the projection bootstrap technique was used to improve accuracy and diversity within decision trees. It was found that 1-day prediction of the three models obtained better performance than 3-, 5-, 7-, and 10-day predictions. The accuracy of the forecasted results degraded as the lead time of the forecast increased. These results are consistent with those of previous studies (Chang et al. 2015).

Another important criterion for model comparison is computation time. In this context, Table 1 lists the training times and complexity for parameter optimization for both regressors. The first row of Table 1 shows the optimal parameter values corresponding to each model. For RF, the number of trees (B) was set to 100 and the number of features, randomly selected at each node (F), was set to three. For CCF-CRF, the number of trees (B) was set to 100 and the number of features (F) to seven. The training times under the optimal parameter configuration were given in M. The time required to perform the parameter optimization is compared in N.

Table 1 Training times in seconds for LS-SVR, RFR, and CCF-CRF
Full size table

Having obtained the optimal parameters, CCF-CRF was found to be 17 times faster than LS-SVR. On 330 training samples, parameter optimization for LS-SVR took nearly 36 times longer than that for CCF-CRF. Pal (2005) reached the same conclusions, whereby LS-SVR was known for having a longer training time than RF because it often requires an optimization phase that is seldom straightforward, but CCF-CRF needs only slight parameter tuning for a short training time for optimization. This is shown in Table 1, where the computation time of the RFR ensemble was small, but Fig. 5 shows that the proposed CCF-CRF was more efficient than RFR in most cases, particularly for long-term predictions. For CCF-CRF, there was a trade-off between performance and computation time.

Comparison between horizons to determine the optimal time lag

The lag times of precipitation, temperature, and historical GWL have a significant influence on the predicted GWL (Yoon et al. 2011). Therefore, based on the results of a comparison among the results reported in the previous subsection, a series of time lags were selected to predict daily GWL using the CCF-CRF model. From Table 2, it is evident that the model with time lag P(t − 2)T(t)H(t) represents the best performance at different horizons during the testing stage, which confirms the retardation effect of GWL fluctuation due to rainfall at this site. This can be attributed to the construction of the aquifer on the site. It was also found that a 1-day yielded obtained better performance than 3-, 5-, 7-, and 10-day predictions. The accuracy of the forecasted results decreased as the lead time of the forecast increased. For a long lag time (7 and 10 days), the CFRC-CCF model with a lag time of P(t − 2)T(t)H(t) performed well, which is consistent with the results shown in Fig. 5.

Table 2 Performance of the CCF-CRF model with different lag times during the testing periods for 1-, 3-, 5-, 7-, and 10-day-ahead groundwater level forecasting for Guxian well station
Full size table

Predicting groundwater level

Once the best model scenario and corresponding time lag were determined, the optimal model was used to predict groundwater levels for 1-, 3-, 5-, 7-, and 10-day forecasts. Based on the best model and the time lag, Fig. 6 shows the scatter plots of optimal models for deferent horizons in the testing period. It is clear that 1-day GWL predictions were less scattered and closer to the straight line than those the other predictions. In general, the CCF-CRF model showed impressive performance with respect to R and RMSE for all horizons. It was also found that it underestimated high GWLs and overestimated low ones in predicting extreme occurrences, as found by Wunsch et al. (2018) and Emamgholizadeh et al. (2014). Therefore, GWL prediction should be divided into low and high levels in case of a rapid drop or rise.

Fig. 6
figure 6

Comparison of observed and predicted groundwater level of the optimal model for 1, 3, 5, 7, and 10 days (corresponding to a–e, respectively) ahead during the testing period

Full size image

It was this verified that the CCF-CRF model with P(t − 2)T(t)H(t) lag time offers relatively good agreement between the observed values and their corresponding measured values.

Conclusions

This paper applied CCF-CRF to short-term GWL prediction at the Guxian well at the groundwater source field of the Daguhe River. To evaluate the effectiveness of CCF-CRF, its accuracy was compared with LS-SVR and RFR, and results show that it can generate a more accurate estimation of GWL for various prediction horizons (1, 3, 5, 7, 10 days). It was also found that the CCF-CRF model offers a better trade-off between prediction performance and computation time than both the other two algorithms. Based on the optimal model, the highest prediction accuracy was achieved using precipitation P(t − 2), temperature T(t), and groundwater level H(t) as time lag. The CCF-CRF yielded excellent performance, particularly over longer prediction horizons with sparser data pairs.

Overall, the results of the case study are favorable and show that CCF-CRF is a promising prediction tool in groundwater hydrology. Moreover, this paper provided case study-based illustrations that show that it is suitable for situations where only low-dimensional input data are available. This study used data from only one station, and more data from other areas can be used to verify the conclusions of this study. Furthermore, research is needed to improve predictive accuracy when there is sudden change in GWL over consecutive time periods.